Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.7 - Ex. 173
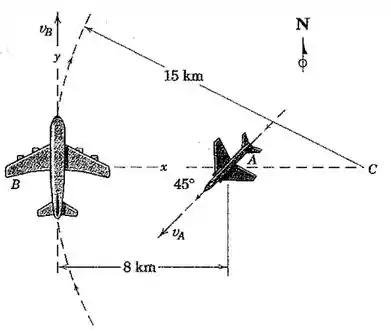
O transporte aéreo B está voando com uma velocidade constante de 800 km/h em um arco horizontal com 15 km de raio. Quando B atinge a posição mostrada, a aeronave A, voando para sudoeste a uma velocidade constante de 600 km/h, cruza a linha radial a partir de B para o centro de curvatura C de sua trajetória. Escreve a expressão vetorial, utilizando os eixos x-y fixados em B, para a velocidade de A quando medida por um observador no interior de B e girando com B.
Passo 1
Pessoal, vamos primeiro passar as velocidades para m/s e calcular a velocidade angular da aeronave B (Em notação vetorial!!).
Agora, vamos usar a equação da velocidade relativa para relacionar as aeronaves:
Substituindo os valores:
Resposta
Exercícios de Livros Relacionados
O disco rola sem deslizar sobre a superfície horizontal, e no instante representado, o centro O possui a velocidade e a aceleração mostradas na figura. Para esse instante, a partícula A possui a veloc
Considere o trilho de uma estrada de ferro reta e horizontal com um vagão ferroviário de 50000kg se deslocando ao longo da linha férrea a uma velocidade constante de 15m/s. Determine a força horizonta
Um veículo A viaja para o oeste em alta velocidade em uma estrada perfeitamente reta B que é tangente à superfície da Terra no equador. A estrada não possui qualquer curvatura no plano vertical. Deter
Ao contornar uma curva sem inclinação lateral a uma velocidade constante de 25 km/h, o centro C do vagão ferroviário segue uma trajetória circular de raio ρ = 60 m . O eixo longitudinal do vagão perma
Um veiculo experimental A viaja com velocidade constante v em relação à Terra ao longo de uma estrada de ferro ligando norte ao sul. Determine a aceleração de Coriolis a c o r em função da latitude θ