Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 122
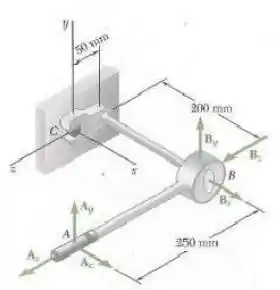
Um mecânico utiliza uma chabe de boca para afrouxar um parafuso em . O mecânico mantém o cabo da chave de boca nos pontos e e aplica forças nesses pontos. Sabendo que essas forças são equivalentes a um sistema força-binário em que consiste em uma força e um binário , determine as forças aplicadas em e quando .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Neste problema, temos o sistema força-bnário e queremos descobrir as forças que geram esse sistema.
O sistema é dado por:
E:
Vamos analisar as forças. Como faz parte do sistema força-binário, podemos afirmar que o somatório das forças em e , resultaram em :
As forças na direção do eixo , são, e . Temos então que:
Na direção do eixo , temos e , portanto:
Na direção do eixo , temos e , portanto:
Como , temos que:
Guarde esses resultados, pois serão importantes para substituirmos no próximo passo.
Passo 2
Para o cálculo do momento resultante em , precisamos calcular os vetores deslociamentos. Para cada ponto em que exista uma força aplicada, existirá um vetor deslocamento com origem em e fim no ponto de aplicação, portanto:
Agora, podemos calcular o momento resultante em , através do produtor vetorial do vetor deslocamento e das forças. Temos que:
Logo:
Resolvendo, temos:
Passo 3
Agora é só avaliar as relações. Temos que:
Da ultima, podemos concluir que:
Substituindo na primeira, temos que:
Logo:
Temos também que:
E:
Substituindo, temos que: