Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 41

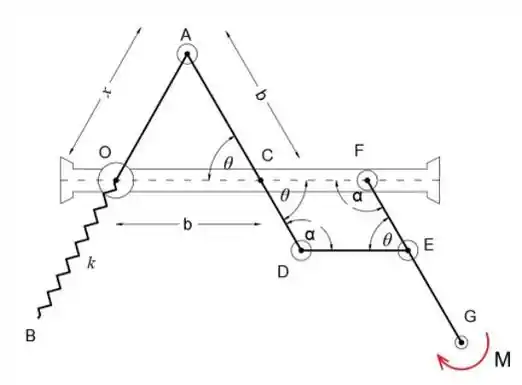
No mecanismo mostrado, a haste AB desliza através do colar articulado em O e comprime a mola quando o par M é aplicado para ligar GF para aumentar o ângulo θ. A mola possui uma rigidez k e seria descomprimida na posição θ = 0. Determine o ângulo θ para o equilíbrio. Os pesos dos links são insignificantes. A Figura CDEF é um paralelogramo.

Passo 1

Primeiro, vamos desenhar o diagrama de força ativa

Observe que há o par M atuando no sistema, há também uma mola acoplada e que a massa é desprezada. Sabendo disso, podemos escrever a equação de equilíbrio

δ U = δ V δ U M = δ V e (1)

Olhando para o triângulo △ OCA e usando a regra do cosseno, podemos expressar a mudança no comprimento da mola x como

x 2 = 2 b 2 - 2 b 2 c o s ⁡ θ

Também podemos notar que CDEF é um paralelogramo, portanto podemos escrever o ângulo α como

a = 180 ∘ - θ

Derive ambos lados da equação para obter

δ α = - δ θ

Podemos escrever um trabalho virtual feito pelo casal M como

δ U M = M δ α

Substituiremos δ α por δ θ

δ U M = - M δ θ (2)

Passo 2

Uma vez que rotulamos a mudança no comprimento da mola como x, a expressão para a energia potencial elétrica é

V e = 1 2 k x 2

Substituiremos x 2 por 2 b 2 - 2 b 2 c o s ⁡ θ

V e = 1 2 k 2 b 2 - 2 b 2 c o s ⁡ θ V e = k b 2 ( 1 - c o s ⁡ θ )

Derivaremos ambos lados da equação

δ V e = k b 2 s i n ⁡ θ δ θ (3)

Passo 3

Substituiremos δ U M e δ V e pelas expressões (2) e (3) nas equações (1)

- M δ θ = k b 2 s i n ⁡ θ δ θ

Expressaremos força s i n ⁡ θ como

s i n ⁡ θ = - M k b 2

Por fim, expressaremos θ como

θ = a r c s i n ⁡ - M k b 2

Resposta

θ = a r c s i n ⁡ - M k b 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A aceleração de uma partícula é diretamente proporcional ao tempo t . Quando t = 0 , a velocidade da partícula é v = 16 m / s . Sabendo que v = 15 m / sex = 20 m quando t = 1 s , determine a velocidad
Determine o valor de equilíbrio de x para a barra sustentada por molas. A mola tem uma rigidez ke não é esticada quando x = 0. A força F atua na direção da barra, e a massa da barra é desprezível.
Para o mecanismo mostrado, a mola é descomprimida quando θ = 0. Determine o ângulo θ para a posição de equilíbrio e especifique a rigidez mínima da mola k que limitará θ a 〖30〗 ^ ∘. A haste DE passa l
A energia potencial de um sistema mecânico é dada porV = 6 x 4 - 3 x 2 + 5 , onde x é a coordenada de posição que define a configuração do sistema de um único grau de liberdade. Determine os valores d
Determine a força Q na mandíbula do cisalhamento para a força 400-N aplicada com θ = 30 ∘. (Dica: substitua a força 400-N por uma força e um par no centro da engrenagem pequena. O deslocamento angular