Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 34
Determine a força Q na mandíbula do cisalhamento para a força 400-N aplicada com θ = 30 ∘. (Dica: substitua a força 400-N por uma força e um par no centro da engrenagem pequena. O deslocamento angular absoluto da engrenagem deve ser determinado cuidadosamente.)
Passo 1
Primeiro. vamos substituir a força de 400 kN pela força e um par agindo no ponto
A, e faremos a mesma coisa para a força Q no ponto O
Observe que os valores dos pares MF e MQ são
Passo 2
Agora, vamos dar uma olhada na geometria do dispositivo por um momento
No esboço abaixo, os pontos D + e D são projeções do ponto D ao longo do tempo, em engrenagens pequenas e grandes, respectivamente
Uma vez que as engrenagens estão conectadas, os comprimentos dos arcos (AD ) ̂ e (DD ) ̂ são os mesmos
Sabendo que o comprimento é um produto do raio e do ângulo, podemos escrever isso como
A partir daqui expressaremos como
Vamos substituir (OD) e (AD) por seus valores para calcular a rotação da engrenagem pequena sobre o ponto A
Passo 3
A seguir, desenharemos o diagrama de força ativa do dispositivo sem rotação (esmaecido) e após a rotação infinitesimal (observe que no esboço o ângulo infinitesimal é excessivamente grande)
Podemos notar três coisas importantes aqui:
- o ponto A é impedido de se mover para baixo da linha OA, portanto, ele se move perpendicularmente ao OA
- o ponto O não se move, portanto, o Trabalho Virtual realizado pela força Q é igual a zero
- engrenagem pequena gira em torno do ponto O, bem como A, portanto, o deslocamento angular absoluto (γ) da engrenagem é
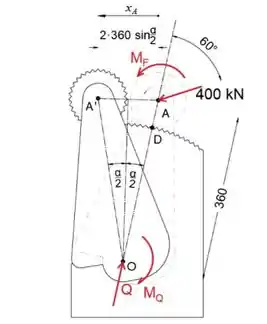
Vamos derivar a expressão para x_A a fim de escrever o deslocamento infinitesimal do ponto A
Como o ângulo α é infinitesimal, podemos dizer que o valor de cosα / 2 é igual a 1. portanto, expressão para é
Vamos usar a expressão derivada para γ a fim de escrever o deslocamento angular infinitesimal da engrenagem pequena
Passo 4
Trabalho Virtual realizado pelo casal MF é produto da Rotação Virtual δγ e do momento que a força produz
Substituiremos por 144000 e by
(1)
Trabalho virtual feito por força é
Substituiremos por
(2)
O trabalho virtual realizado pelo casal MQ é negativo porque o sentido de rotação é oposto ao sentido de casal
Substituiremos por
(3)
Próximo, nós aplicamos o Princípio do Trabalho Virtual, que afirma que a soma do trabalho realizado por todas as forças ativas é igual a zero
Substituiremos e pelas expressóes e respectivamente
Dividiremos ambos lados da equação por
Por fim, a força Q da mandíbula é