Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 36

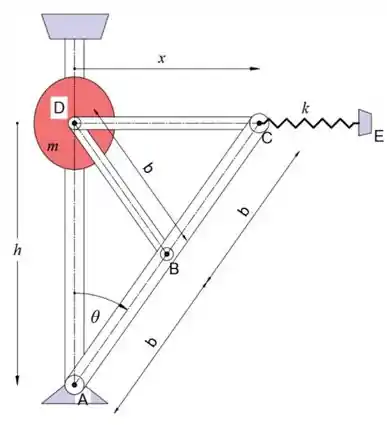
Para o mecanismo mostrado, a mola é descomprimida quando θ = 0. Determine o ângulo θ para a posição de equilíbrio e especifique a rigidez mínima da mola k que limitará θ a 〖30〗 ^ ∘. A haste DE passa livremente através do colar pivotado C, e o cilindro de massa m desliza livremente no eixo vertical fixo.

Passo 1

Primeiro, vamos desenhar o diagrama de força ativa

Observe que não há forças externas atuando, portanto, a equação de equilíbrio é

δ V = 0

δ V g + δ V e = 0 (1)

Expressão da energia potencial gravitacional

V g = 2 m g h

A partir do esboço podemos ver que h = 2 b c o s ⁡ θ

V g = 2 m g b c o s ⁡ θ

Derive ambos lados da equação para obter

δ V g = - 2 m g b sin ⁡ θ (2)

Passo 2

Uma vez que a energia potencial elástica é

V e = 1 2 k x 2

Percebemos do esboço que x = 2 b s i n ⁡ θ

V c = 1 2 k ( 2 b s i n ⁡ θ ) 2 V e = 4 b 2 2 k s i n 2 ⁡ θ V c = 2 b 2 k s i n 2 ⁡ θ

Derive ambos lados da equação

δ V e = 2 b 2 k ( 2 s i n ⁡ θ c o s ⁡ θ ) δ V e = 4 b 2 k s i n ⁡ θ c o s ⁡ θ (3)

Substituiremos V g e V e pelas expressões (2) e (3) na equação (1)

- 2 m g b s i n ⁡ θ + 4 b 2 k s i n ⁡ θ c o s ⁡ θ = 0 2 s i n ⁡ θ - m g b + 2 b 2 k c o s ⁡ θ = 0

Diremos que o mecanismo presente no equilíbrio é 1 :     s i n ⁡ θ = 0

θ = 0

2:  - m g b + 2 b 2 k c o s ⁡ θ = 0

c o s ⁡ θ = m g b 2 b 2 k

θ = a r c c o s ⁡ m g 2 b k

Passo 3

A partir da expressão c o s ⁡ θ = m g b 2 b 2 k podemos expressar a rigidez da mola k como

k = m g 2 b c o s ⁡ θ

Substituiremos cosθ por seu valor a fim de determinar a rigidez mínima k necessária para limitar o mecanismo

k = m g 2 b 3 2 k = m g b 3

Resposta

θ = a r c c o s ⁡ m g 2 b k k = m g b 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se a mola tem rigidez à torção de k = 300N ⋅ m / r a d e encontra-se não deformada quando θ = 90 ° , determine o ângulo θ quando a estrutura está em equilíbrio.
A janela de atendimento em um restaurante consiste em portas de vidro acionadas automaticamente por um motor que fornece um torque M a cada porta. As extremidades, A e B , se movem ao longo das guias
Quando θ = 30 ° , o bloco uniforme de 25k g comprime as duas molas horizontais em 100m m . Determine a intensidade dos momentos de binário aplicados M necessários para manter o equilíbrio. Considere k
O elemento esbelto de peso W se apoia na parede e no piso lisos. Determine a intensidade da força P necessária para mantê-lo em equilíbrio para determinado ângulo θ .
O “pantógrafo de Nuremberg” está sujeito a uma força horizontal P=600N . Determine a rigidez k da mola para o equilíbrio quando θ = 60 ° . A mola não está esticada quando θ = 15 ° .