Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 54
O pêndulo invertido de massa me centro de massa G é sustentado pelas duas molas, cada uma de rigidez k. Se as molas estiverem igualmente esticadas quando o pêndulo estiver na posição vertical mostrada, determine as posições de equilíbrio estático e investigue a estabilidade do sistema em cada posição. Considere as molas suficientemente compridas para que permaneçam efetivamente na horizontal.
Passo 1
O enunciado pede que a gente determine as posições de equilíbrio estático e investigue a estabilidade do sistema em cada posição.
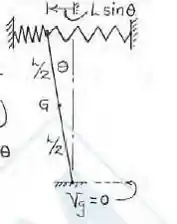
Passo 2
Para equilíbrio
Para
Então
Resposta
Exercícios de Livros Relacionados
A junta articulada está sujeita à carga P . Determine a força compressiva F que ela cria sobre o cilindro em A em função de θ .
A mola conectada ao mecanismo não tem deformação quando θ = 90 ° . Determine a posição θ para haver equilíbrio e investigue a estabilidade do mecanismo nessa posição. O disco A é conectado por pino à
A haste uniforme A B tem massa de 50k g . Se as duas molas D E e B C não estão deformadas quando θ = 90 ° , determine o ângulo θ para haver equilíbrio usando o princípio da energia potencial. Investig
A haste uniforme A B tem massa de 5k g . Se a mola conectada não está deformada quando θ = 90 ° , determine o ângulo θ de equilíbrio usando o método do trabalho virtual. Observe que a mola sempre perm
Os elementos uniformes A B e B C possuem massa de 1k g cada e o cilindro possui 10k g . Determine a força horizontal P necessária para manter o mecanismo em posição quando θ = 45 ° . A mola tem compri