Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 37

A barra uniforme de massa m e comprimento L é suportada no plano vertical por duas molas idênticas, cada uma de rigidez k e comprimida a uma distância δ na posição vertical θ = 0. Determine a rigidez mínima k que garantirá uma posição de equilíbrio estável com θ = 0. Pode-se assumir que as molas atuam na direção horizontal durante o pequeno movimento angular da barra.

Passo 1

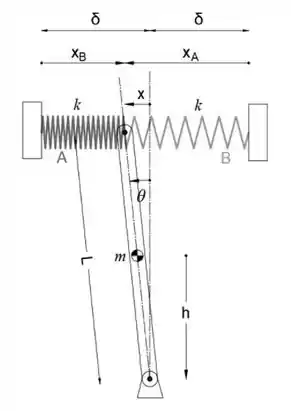
Primeiro. vamos desenhar o diagrama de força ativa

Observe que não há forças externas agindo, portanto, podemos escrever a equação de equilíbrio como

δ V = 0   δ V g + δ V e = 0 (1)

Podemos ver no esboço que as distâncias x e h são

x = L s i n ⁡ θ h = L 2 c o s ⁡ θ

Embora a mudança no comprimento das molas A e B sejam

x A   = δ + x   = δ + L s i n ⁡ θ x B   = δ - x   = δ - L s i n ⁡ θ

Expressão para energia potencial gravitacional

V g = m g h

Substituiremos h por L c o s ⁡ θ

V g = 1 2 m g L c o s ⁡ θ

Derive ambos lados da equação para obter

δ V g = - 1 2 m g L s i n ⁡ θ δ θ (2)

Passo 2

Uma vez que temos duas molas ligadas ao sistema, podemos escrever a expressão para a energia elástica potencial como

V e = 1 2 k x A 2 + x B 2

Substituiremos x A e x B pelas expressões δ + L s i n ⁡ θ e δ - L s i n ⁡ θ , respectivamente

V e = 1 2 k ( δ + L s i n ⁡ θ ) 2 + ( δ - L s i n ⁡ θ ) 2 V e = 1 2 k 2 δ 2 + 2 L 2 s i n 2 ⁡ θ V e = k δ 2 + L 2 s i n 2 ⁡ θ

Derive ambos lados da equação

δ V e = k L 2 ( 2 s i n ⁡ θ c o s ⁡ θ ) δ θ (3)

A seguir, substituiremos δVg e δVe pelas expressões (2) e (3) na equação de equilíbrio (1)

- 1 2 m g L s i n ⁡ θ + k L 2 ( 2 s i n ⁡ θ c o s ⁡ θ ) = 0

Observe que o sistema é estável quando a segunda derivada da equação de equilíbrio é maior que zero

- 1 2 m g L s i n ⁡ θ + k L 2 ( 2 s i n ⁡ θ c o s ⁡ θ ) d V d θ > 0 - 1 2 m g L c o s ⁡ θ + 2 k L 2 c o s 2 ⁡ θ - s i n 2 ⁡ θ > 0 (4)

Passo 3

Para verificar a estabilidade da posição θ = 0, vamos simplesmente colocar o valor de θ em (4)

- 1 2 m g L c o s ⁡ 0 ∘ ⏞ - 1 + 2 k L 2 c o s 2 ⁡ 0 ∘ ⏞ - 1 - s i n 2 ⁡ 0 ∘ ⏞ - 0 ) > 0 - 1 2 m g L + 2 k L 2 > 0

A partir daqui, podemos expressar a rigidez da mola k como

k > 1 2 m g L 2 L 2

k > m g 4 L

Portanto, podemos dizer que a rigidez mínima da corda necessária para garantir a estabilidade é

k min  = m g 4 L

Resposta

k m i n = m g 4 L

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a força F entre as mandíbulas da braçadeira em termos de um torque M exercido na alça do parafuso de ajuste. O parafuso tem avanço (avanço por rotação) L e o atrito deve ser desprezado.
Ao testar o projeto do macaco de levantamento de recurso, 12 voltas da alça são exigidos para elevar a almofada de levantamento 1 pol. Se uma força F = 10 lb aplicada normal à manivela para necessária
Uma meia seção do tubo de massa m e raio r é liberada do repouso na posição mostrada. Sabendo que o tubo rola sem deslizar, determine (a) sua velocidade angular depois de ter rolado 90 °, (b) a reação
Uma barra delgada de comprimento l e peso W é pivotada em uma extremidade como mostra a figura. Ela é liberada do repouso na posição horizontal e oscila livremente. (a) Determine a velocidade angular
A elevação da plataforma de massa m suportada pelos quatro elos idênticos é controlada pelos cilindros hidráulicos AB e AC que são articulados no ponto A. Determine a compressão P em cada um dos cilin