Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 11.Problemas fundamentais - Ex. 6
O mecanismo pantográfico está sujeito a uma força P=150 N. Determine o ângulo para o equilíbrio. A mola está livre em . Despreze a massa dos membros.
Passo 1
Desenhando o diagrama do corpo livre:
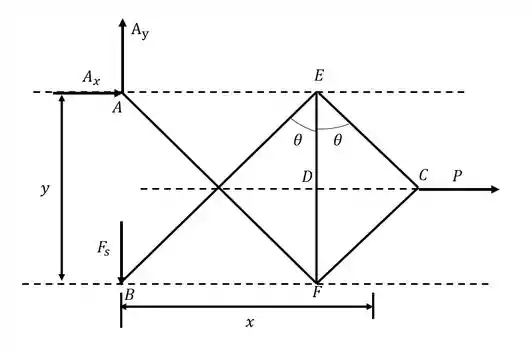
Passo 2
Desenhando o diagrama dos deslocamentos virtuais: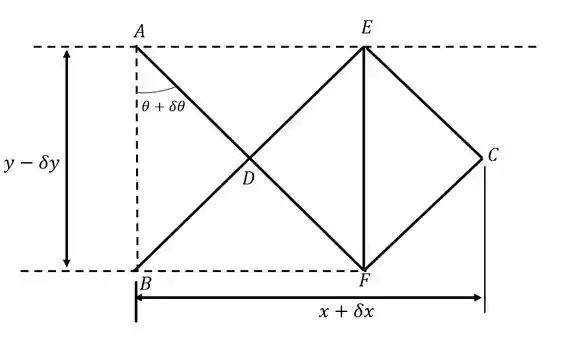
Passo 3
O primeiro passo é definir as coordenadas dos pontos de interesse:
Passo 4
Podemos definir a elongação inicial da mola:
A mola está descompressa em
Passo 5
Podemos calcular a força da mola para um ângulo genérico :
Passo 6
Tomando a derivada das posições x e y para obter-se os deslocamentos virtuais:
Passo 7
Aplicando a equação do trabalho virtual:
Essa equação não possui solução analítica. Deve-se utilizar um software gráfico ou o método da tentativa e erro:
Resposta
Exercícios de Livros Relacionados
8. Uma mola de constante 15N / c m é presa a pinos nos pontos C e F tal como mostra a figura. Desprezando o peso da mola e do mecanismo articulado, determine a força na mola e o deslocamento vertical
19- Uma força P de 4k N é aplicada tal como mostra a figura ao pistão de um sistema motor. Sabendo que A B = 50m m e B C = 200m m , determine o binário M necessário para se manter o equilíbrio do sist
18- O pino em C é preso ao elemento B C D e pode deslizar ao longo de uma fenda aberta na placa fixa mostrada na figura. Desprezando o efeito do atrito, deduza uma expressão para a intensidade do biná
Para o mecanismo articulado mostrado na figura, determine a força Q nescessario para o equilíbrio, quando l = 450m m , Q = 180N ⋅ m m e θ = 65 ° .
Um binário M de intensidade 100N ⋅ M é aplicado, tal como mostra a figura, à manivela de um sistema motor. Sabendo que A B = 50m m e B C = 200m m , determine a força P necessária para se manter o equi