Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 20
Um binário M de intensidade é aplicado, tal como mostra a figura, à manivela de um sistema motor. Sabendo que e , determine a força necessária para se manter o equilíbrio do sistema, quando (a) , (b) .
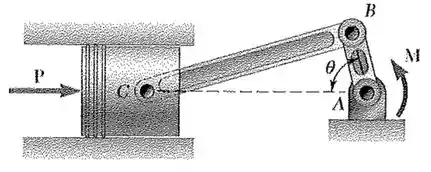
Passo 1
Primeiro, vamos fazer uma lei dos senos, depois de analisar a geometria do problema!
Passo 2
Vamos agora definir os parâmetros para o trabalho virtual! Sendo a base (CA), temos que:
Da equação do passo 1, temos que:
Ou
Da equação derivada da base:
Ou
Logo,
Passo 3
Legal galera, achamos os termos do trabalho virtual em função dos ângulos! Vamos aplicar a formula do trabalho virtual!
Portanto,
Passo 4
Agora basta aplicarmos os valores de cada alternativa e acabamos com a questão!
- ,
,
Resposta
Exercícios de Livros Relacionados
O disco está sujeito a um momento de binário M . Determine a rotação θ do disco necessária para que haja equilíbrio. A extremidade da mola envolve o perímetro do disco enquanto ele gira. A mola está o
Os colares A e B partem do repouso e o colar A se movimenta para cima com uma aceleração de 60 t ² m m / s ² ² ². Sabendo que o colar B se movimenta para baixo com aceleração constante e que sua veloc
Determine o torque M na alavanca de ativação do caminhão basculante necessário para equilibrar a carga de massa m com o centro de massa em G quando o ângulo de despejo é θ. O polígono ABDC é um parale
Determine a força vertical P necessária para manter o equilíbrio da ligação no plano vertical na posição θ. Cada elo é uma barra uniforme com massa ρ por unidade de comprimento. Mostre que P é indepen
Encontre a força Q exercida no papel pelo perfurador de papel do Prob. 4/89, repetido aqui.