Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 19

19- Uma força P de 4   k N é aplicada tal como mostra a figura ao pistão de um sistema motor. Sabendo que A B = 50   m m e B C = 200   m m , determine o binário M necessário para se manter o equilíbrio do sistema, quando a θ = 30 ° , b θ = 150 ° .

Passo 1

Vamos desenhar o sistema de coordenadas no ponto de aplicação do momento e utilizando o valor θ sendo uma ângulo agudo tal como é dito na letra a.

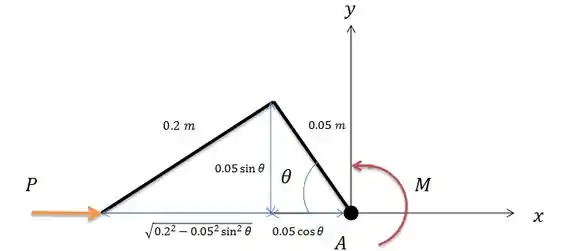
Onde o momento   M tende a diminuir o ângulo θ então o trabalho virtual gerado por ela será igual a:

δ U M = - M d θ

E o trabalho virtual gerado pela força P por diminuir sua linha de ação será:

δ U P = P   d 0.05 cos ⁡ θ + 0.04 - 0.0025 sin 2 ⁡   θ

Fazendo essa derivada em relação a θ temos:

δ U p = P - 0.05 sin ⁡ θ   d θ + 1 2 0.04 - 0.0025 sin 2 ⁡   θ × - 2 × 0.0025 × sin ⁡ θ cos ⁡ θ   d θ

δ U p = P - 0.05 sin ⁡ θ - 1.25 × 10 - 3 sin ⁡ 2 θ 0.04 - 0.0025 sin 2 ⁡   θ   d θ

Passo 2

Dessa forma para θ = 30 ° e P = 4 k N   temos:

δ U = δ U M + δ U p = 0

M = - 4 × 10 3 - 0.05 sin ⁡ 30 - 1.25 × 10 - 3 sin ⁡ 60 0.04 - 0.0025 sin 2 ⁡   30   = 121.82   N m

Passo 3

Agora para um ângulo obtuso, tal como na letra b.

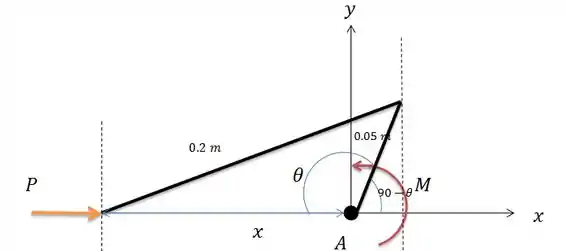
Temos que descobrir o valor de x para encontrar o trabalho virtual causado por P em relação a A . Para isso vamos destacar esse triangulo obtuso.

Como sin ⁡ - 90 - θ = - sin ⁡ 90 - θ = - cos ⁡ θ   ou | - cos ⁡ θ | = cos ⁡ θ

E

cos ⁡ - 90 - θ = cos ⁡ 90 - θ = sin ⁡ θ

Então teremos:

x = 0.2 2 - 0.05 2 sin 2 ⁡ θ - 0.05 cos ⁡ θ

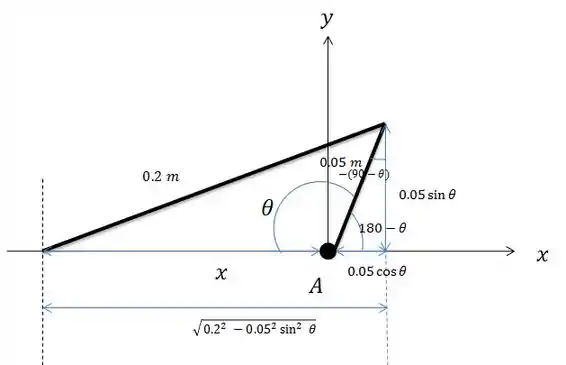
O que nos dá uma distância diferencial igual a:

d x = 0.05 sin ⁡ θ - - 0.0025 sin ⁡ 2 θ 2 0.04 - 0.0025 sin 2 ⁡ θ  

d x = 0.05 sin ⁡ θ + 0.00125   s i n   2 θ 0.04 - 0.0025 sin 2 ⁡ θ d θ

Passo 4

Então o trabalho virtual para θ = 150 ° será:

M = P 0.05 sin ⁡ θ + 0.00125   s i n   2 θ 0.04 - 0.0025 sin 2 ⁡ θ d θ

M = 78.18   N m

Resposta

a )   M = 121.82   N m

b )   M = 78.18   N m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A talha portátil de carro é operada pelo sistema hidráulico cilindro que controla a horizontalmovimento da extremidade A do elo na ranhura horizontal. Determine a compressão C no pistão haste do cilin
Cada uma das quatro barras móveis uniformes tem uma massa m, e sua posição de equilíbrio na vertical plano é controlado pela força P aplicada ao final da barra inferior. Para um determinado valor de P
A caixa de carga do caminhão de entrega de alimentos para aeronaves a manutenção tem uma massa carregada m e é elevada pela aplicação de um torque M na extremidade inferior do elo que é articulado à e
Determine o par M necessário para manter o equilíbrio em um ângulo θ . Cada uma das duas barras uniformes tem massa m e tem comprimento l.Fonte: Meriam - Estática - 7ª ed
A massa da barra uniforme de comprimento l é m enquanto a da barra uniforme de comprimento 2l é 2m. Para uma dada força P, determine o ângulo θ de equilíbrio.Fonte: Meriam - Estática - 7ª ed