Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 159
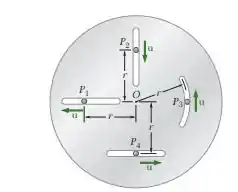
15.159. Resolva o Problema 15.158 admitindo que a placa gire em torno de O com velocidade angular constante , no sentido horário.
Passo 1
A diferença mais significante entre esse problema e o de antes é a direção da força de Coriolis. Mas vamos repetir todo o racioinio.
A gente pode usar uma equação geral para todos os pinos:
Nessa equação temos
: aceleração do pino;: ;: aceleração relativa entre o pino e a placa;: aceleração de Coriolis .
Passo 2
Para os pinos e temos que
A aceleração relativa com a placa é nula. Mas para complicar um pouquinho as coisas o pino possui uma aceleração relativa não nula.
E todos os pinos possuem uma aceleração de Coriolis com módulo de . A direção é sempre perpendicular a no sentido de , ou seja, no sentido horário.
Passo 3
Agora vamos começar a calcular as acelerações:
Olha só as componentes são na direção de e a força de Coriolis, como a velocidade está apontando para , essa aceleração tem que estar em .
Seguindo esse raciocínio, vamos fazer
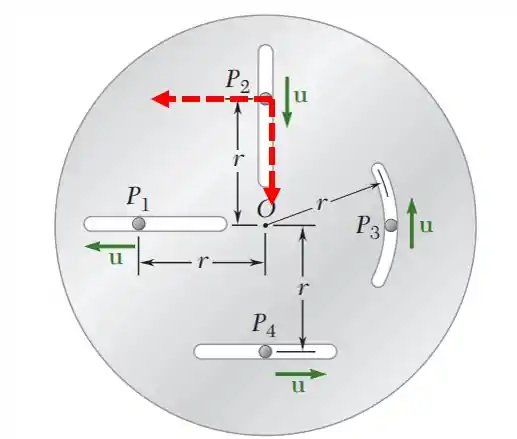
Agora para o pino vamos ter uma diferença, a aceleração relativa:
A aceleração relativa é no sentido de .
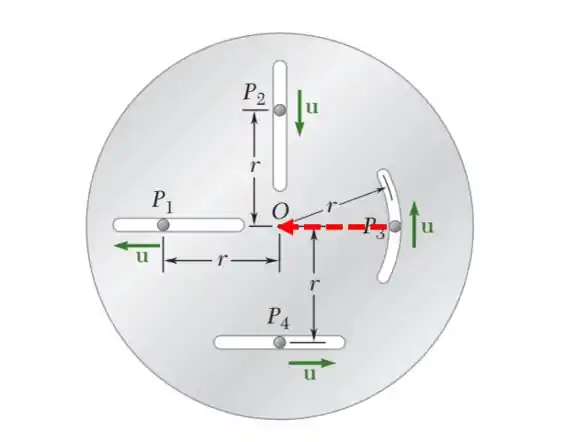
Então
E agora finalmente o pino
Então