Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.6 - Ex. 117

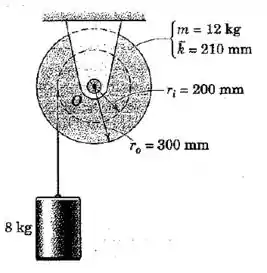
A velocidade do cilindro de 8   k g é de 0,3   m / s em um determinado instante. Qual é a sua velocidade v após uma queda adicional de 1,5   m ? A massa do tambor com o seu encaixe é de 12   k g , seu raio de giração centroidal é de k - = 210   m m , e o raio do seu encaixe é r i = 200   m m . O momento de atrito em O é constante em 3   N ∙ m .

Passo 1

Vamos começar calculando a energia cinética do sistema nesse instante inicial:

T 1 = T c i l i n d r o + T t a m b o r

T 1 = 1 2 m v 2 + 1 2 I ω 2

E podemos substituir ω = v / r e I = m k - 2 , então:

T 1 = 1 2 8 0,3 2 + 1 2 12 0,210 2 0,3 0,2 2

T 1 = 0,955   J

E vamos escrever também uma equação para o caso em que o sistema atinge a velocidade final v após uma queda de 1,5   m :

T 2 = 1 2 m v 2 + 1 2 I v r 2

T 2 = 1 2 8 v 2 + 1 2 12 0,210 2 v 0,2 2

T 2 = 4 v 2 + 6,62 v 2 = 10,62 v 2

Passo 2

Agora vamos escrever a lei de conservação de energia entre esses dois instantes (antes e depois da queda de 1,5   m ):

T 1 + V 1 = T 2 + V 2 + E d i s s

E vamos colocar o zero da energia potencial no ponto que o cilindro atinge ao descer os 1,5   m adicionais, então:

V 2 = 0

V 1 = m c i l i n d r o g 1,5 = 8 9,81 1,5 = 117,72   J

E a energia E d i s   dissipada pelo momento de atrito pode ser calculada usando a fórmula para o trabalho de um momento:

E d i s s = M Δ θ = 3 1,5 0,2 = 22,5   J

Agora é só substituir tudo na equação principal:

0,955 + 117,72 = 10,62 v 2 + 22,5

10,62 v 2 = 96,175

v = 3,01   m / s

Resposta

A sua velocidade será v = 3,01   m / s 2 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O mecanismo mostrado se move no plano vertical. A barra vertical AB tem uma massa de 4,5 kg, e cada uma das duas hastes tem uma massa de 2,7kg com centro de massa em G e com um raio de giração de 250
O mecanismo é constituído por duas barras esbeltas e se move no plano horizontal sob influência da força P . A barra O C tem uma massa m e a barra A C tem massa 2 m . O bloco deslizante em B tem massa
163. Cada uma das barras uniformes O A e O B possui uma massa de 2k g e é articulada livremente em O ao eixo vertical, que recebe uma aceleração constante a = g / 2 . As hastes que conectam o cursor l
O tacômetro mecânico mede a velocidade de rotação N do eixo pelo movimento horizontal do cursor B ao longo do eixo que gira. Esse movimento é causado pela ação centrífuga das duas massas A de 350 g, q
A plataforma móvel de trabalho é elevada por meio de dois cilindros hidráulicos articulados nos pontos C. A pressão em cada cilindro produz uma força F. A plataforma, o homem e a carga têm uma massa c