Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 2.Problemas - Ex. 23

Uma partícula de massa m = 1   k g está sujeita a uma força unidimensional F t = k t e - α t , onde k = 1 N s   e α = 0,5   s - 1 . Se a partícula estiver inicialmente em repouso, calcule e elabore um gráfico, com a ajuda de um computador, da posição, velocidade e aceleração da partícula como função do tempo.

Passo 1

E aí galera, vamos iniciar mais uma questão do nosso livro!

Primeiramente vamos anotar alguns dados importantes fornecido na questão:

m = 1   k g

α = 0,5   s - 1

k = 1 N s

F = k t e - α t

Lembrando da equação do movimento de Newton:

m a = F n e t

Para força unidimensional, temos:

m a = F = k t e - α t

Assim, a aceleração é dada por:

a t = k m t e - α t

E plotando o gráfico da função temos:

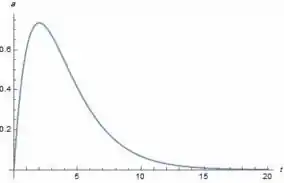
Passo 2

Em seguida, para encontrar a velocidade dessa partícula vamos integrar a equação da aceleração, dessa forma, temos:

v t = ∫ a ( t ) d t

=   ∫ k m t e - α t d t

Podemos resolver por integral por partes ou utilizar um software computacional, dessa forma encontramos:

v t = - k m 1 - e - α t ( 1 + α t ) α 2

Plotando o gráfico da função temos:

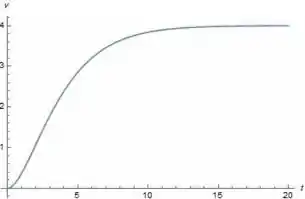
Passo 3

Por fim, para encontrar a posição da partícula iremos integras a equação da velocidade, assim:

x t = ∫ v ( t ) d t

=   ∫ - k m 1 - e - α t 1 + α t α 2 d t

x t = k m t ( 1 - e - α t ) α 2

Plotando o gráfico da equação temos:

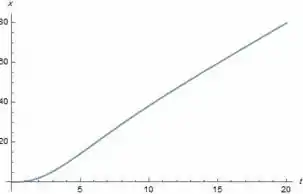
Finalizamos aqui nossa questão, tudo beleza? Te vejo na próxima!

Resposta

a t = k m t e - α t

v t = - k m 1 - e - α t ( 1 + α t ) α 2

x t = k m t ( 1 - e - α t ) α 2

Exercícios de Livros Relacionados

A velocidade de uma partícula que se desloca em linha reta está diminuindo, a uma taxa de 3m / s por metro de deslocamento, em um instante quando a velocidade é de 10m / s . Determine a aceleração a d
Repita o Exemplo 2.4 efetuando um cálculo no computador para resolver a equação 2.22. Use os valores a seguir: m = 1 k g , v 0 = 10 m / s , x 0 = 0 e k = 0,1 s - 1 . Elabore gráficos de v versus t , x
Uma partícula de massa m desliza para baixo sobre um plano inclinado sob a influência da gravidade. Se o movimento estiver sujeito a uma força resistiva f = k m v 2 , demonstre que o tempo necessário
Considere um projétil disparado verticalmente em um campo gravitacional constante. Para as mesmas velocidades iniciais, compare os tempos necessários para que o projétil alcance sua altura máxima (a)