Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 28
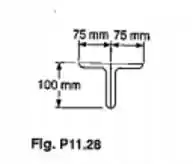
Um membro em compressão, de comprimento efetivo igual a 3,6m, é feito soldando-se juntos dois perfis laminados de aço L100X75X6,35mm, como mostrado. Usando-se E=200GPa, determinar a carga centrada admissível para o membro, se um coeficiente de segurança de 2,5 é desejado.
Passo 1
Fala aí, bora fazer esse exercício de peso admissível.
Beleza, até aqui a gente calculou bastante peso crítico que era dado por:
O peso admissível é parecido, é uma parcela do peso crítico que é aceitável para um determinado fator de segurança e pode ser calculado assim:
Maneiro, temos quase tudo nessa brincadeira, vamos ter que correr atrás do momento de inércia da seção.
Passo 2
Já te digo de cara que não vá perdendo seu tempo calculando esse tipo de momento de inércia á mão, esses perfis possuem um raio interno característico dos perfis L que não podem ser bem aproximados por retângulos. Sendo assim vamos caçar nas tabelas do fim do livro o valor do momento de inércia para o perfil mostrado.
O equivalente ao perfil apresentado é o perfil L102x76x6,4mm retirado da tabela do apêndice C para cantoneiras de abas desiguais.
Temos:
E:
E agora é hora de fazermos a composição do momento de inércia do nosso perfil que é formado por dois perfis do tipo L e aqui usaremos:
E
Onde:
é a área da seção:
é a distância entre os eixos, central do sistema e de cada peça que são simétricas.
Ambos os valores são retirados da mesma tabela:
E a distância dos eixos vai ser no eixo x da figura.
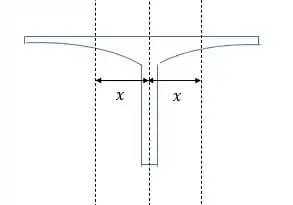
Voltando a equação do momento de inércia substituindo os valores temos:
E aí:
E:
Sendo assim então o usaremos por se tratar do eixo fraco.
Passo 3
Daqui, podemos voltar ao peso crítico:
Substituindo os valores, temos:
E para o peso admissível com o fator de segurança de 2,5: