Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 33
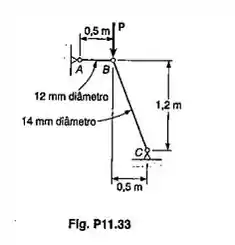
Sabendo-se que um coeficiente de segurança de 2,6 é desejado determinar a maior carga P que pode ser aplicada a estrutura mostrada. Usar E=200GPa e considerar somente flambagem no plano da estrutura.
Passo 1
Fala aí, bora fazer essa questão de flambagem?
Aqui o nosso pensamento deve ser o seguinte, aquela carga P não é a causadora direta da flambagem, as reações nos apoios é que serão responsáveis e vale lembrar que somente esforços de compressão, sendo assim vamos fazer um diagrama de corpo livre e vamos começar pela barra BC.
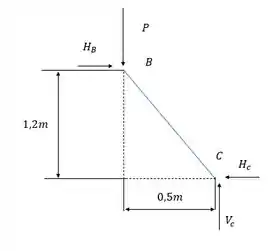
Dessa barra a gente transfere para a barra AB, o esforço horizontal em B que será resistido.
Analisando os nossos diagramas a gente vê os esforços que podem causar compressão e com isso flambagem, vamos ter que analisar as duas barras e calcular os pesos críticos de cada uma pois possuem propriedades geométricas diferentes. Lembrando que a relação entre o peso crítico e o peso admissível é o fator de segurança:
E que pro peso crítico é dado por:
Passo 2
Vamos calcular a reação horizontal em B, a gente pode pegar a estrutura no ponto C e fazer o somatório dos momentos, considerando positivo o sentido horário:
Essa reação nos dá pelo somatório dos esforços horizontais que:
Beleza e com isso a gente descobre pelos esforços verticais que:
Com a geometria da figura podemos calcular a resultante causadora de compressão na barra BC, a gente pode dizer como as forças são perpendiculares que:
Daí:
Passo 3
Temos enfim que o peso crítico é o cara que causa flambagem, tá isso a gente sabe, mas e se a gente considerar que BC flamba?
E:
Sendo assim:
E como a seção é circular temos:
E o comprimento da barra a gente tira fazendo Pitágoras:
E aí:
Sendo assim temos:
E como calculamos:
E enfim:
Passo 4
A outra possibilidade que temos de avaliar é a barra AB, então vamos pensar o seguinte a gente precisa conseguir uma relação entre a horizontal que atua na barra e o peso.
Nesse caso vemos que:
Daí podemos partir pro mesmo processo, se a horizontal causa flambagem ela é o peso admissível, pois precisa do fator de segurança então:
Lembrando que:
Para o peso crítico precisaremos calcular o momento de inércia, dado por:
E temos o comprimento efetivo da barra .
Enfim:
Substituindo o valor:
E rearrumando:
Portanto vamos considerar aqui o menor valor para o qual ocorre flambagem que é na barra BC: