Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 8
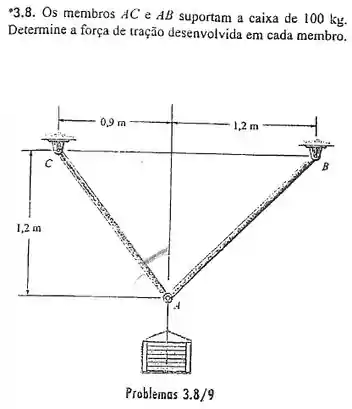
Os membros AC e AB suportam a caixa de 100 kg. Determine a força de tração desenvolvida em cada membro.
Passo 1
Cara, ele quer a tração em cada cabo. A gente pode achar isso usando as equações de equilíbrio no ponto A, já que esse ponto está paradinho.
Vamos fazer o diagrama de corpo livre do nó , para calcularmos as intensidades das forças nos cabos BC e BD:
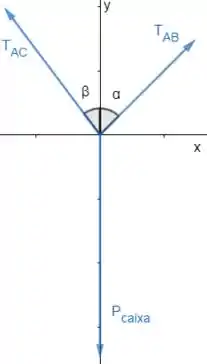
Passo 2
Precisamos descobrir o valor desses ângulos. Podemos descobrir e usando as relações trigonométricas:
Olha na figura, o ângulo tem como cateto oposto o segmento de e como cateto adjacente, o segmento de :
Aqui você também poderia perceber que esse triângulo que contem esse ângulo é proporcional ao triângulo 3/4/5. Aí fica a seu critério mesmo.
Já para o ângulo , ambos os catetos valem :
E o peso da caixa é igual à sua massa vezes a gravidade:
Passo 3
A soma de forças em e em deve ser zero.
Vamos decompor primeiro as forças em :
Como os ângulos que a gente definiu estão opostos ao eixo , ao decompor as forças, as multiplicamos pelo seno de cada ângulo. Repara também que vai estar no sentido negativo de :
Passo 4
Agora vamos decompor as forças em :
Aqui usamos cosseno para decompor as forças porque os ângulos estão colados em . E vemos também que não precisamos decompor a força peso.
Sabemos o valor de , de , de e de , vamos substituir tudo na equação:
Repara que apareceu ali cosseno de 45 sobre seno de 45. Cosseno sobre o seno é igual a um sobre a tangente:
Então
É só a gente calcular esses valores das funções trigonométricas e isolar para achar:
Passo 5
Agora que temos vamos usar a equação que achamos no Passo 3 para descobrir