Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 4

Passo 1

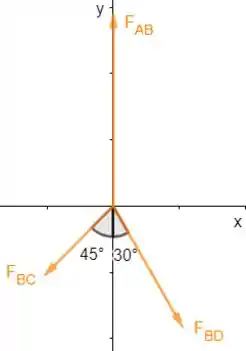
Vamos fazer o diagrama de corpo livre para o nó B:

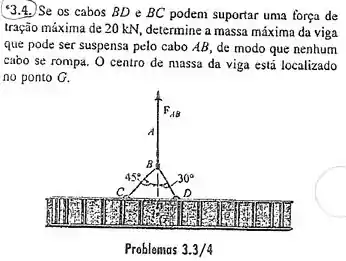
Perceba que a força F_A B está suportanto a viga inteira, então

F_A B = P

onde P é o peso da viga.

F_A B = m g

Passo 2

Como tudo isso ai tem que estar parado, a soma de forças em x e em y deve ser zero.

Vamos decompor as forças em x :

sum F_x = 0

F_B D sen 30 - F_B C sen 45 = 0

(F_B D)/(2) - (sqrt(2) F_B C)/(2) = 0

F_B D - sqrt(2) F_B C = 0

F_B D = sqrt(2) F_B C

Aqui nós percebemos que a tração no cabo BD sempre será maior que a do cabo BC, dessa forma o BC nunca poderá chegar a sofrer uma tração de 20 k N , pois de isso acontecesse o cabo BD iria se romper.

Então a situação mais critica possível seria quando o cabo BD estivesse suportando um tração de 20 k N , nesse caso o BC iria suportar:

20 = sqrt(2) F_B C

F_B C = (20)/(sqrt(2))

F_B C = 14,1 k N

Passo 3

Agora vamos decompor as forças em y para achar o peso máximo da viga:

sum F_y = 0

F_A B - F_B C cos 45 ° - F_B D cos 30 ° = 0

F_A B - (sqrt(2) F_B C)/(2) - (sqrt(3) F_B D)/(2) = 0

F_A B = (sqrt(2) F_B C)/(2) + (sqrt(3) F_B D)/(2)

F_A B = (sqrt(2) F_B C + sqrt(3) F_B D)/(2)

Como vimos no Passo anterior F_A B = m g , substituindo:

m g = (sqrt(2) F_B C + sqrt(3) F_B D)/(2)

m = (sqrt(2) F_B C + sqrt(3) F_B D)/(2 g)

Agora é só substituir os valores encontrados no Passo anterior e o valor da gravidade:

m = (sqrt(2) (14,1 k N) + sqrt(3) (20 k N))/(2 (9,81))

m = 2,78 * 10^3 k g

Resposta

m = 2,78 * 10^3 k g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A tesoura para poda mostrada na figura consiste em duas lâminas e dois cabos. Os dois cabos da ferramenta estão ligados pelo pino C , e as duas lâminas estão ligadas pelo pino D . A lâmina da esquerda
Determine a intensidade das forças de aperto exercidas ao longo da linha a a sobre a porca quando se aplicam duas forças de 225 N nos cabos da ferramenta, tal como mostra a figura. Suponha que os pino
O movimento da pá carregadeira da retroescavadeira mostrada na figura é controlado pelos cilindros hidráulicos A D ,C GeE F . Para cada tentativa de retirar uma parte do calçamento, uma força P de 9 k
A pá carregadeira do trator de carregador frontal mostrado na figura sustenta uma carga de 14,5 k N . O movimento da caçamba é controlado por dois mecanismos idênticos, dos quais apenas um é mostrado.
O movimento da pá carregadeira do trator de carregador frontal mostrado na figura é controlado por dois braços e um acoplamento unidos por pinos em D . Os braços estão localizados simetricamente em re