Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 71
Os membros de um suporte são conectados por um pino na junta O. Determine a intensidade de e seu ângulo para o equiíbrio. Considere .
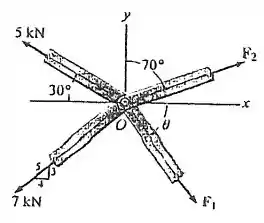
Passo 1
Para encontrar a força e o ângulo, sabe-se que deve ser feita a análise e o equilíbrio de forças no plano bidimensional, ou seja, em x e y.
Passo 2
Logo, o equilíbrio requer que:
Adotando como sentido positivo os sentidos para a direita (eixo x) e para cima (eixo y):
Passo 3
Com a equação (1) e (2) obtém-se:
Igualando as duas equações:
Resposta
Exercícios de Livros Relacionados
Determine a força em cada cabo e a força F necessária para manter a luminária de 4 kg na posição mostrada. Dica: primeiro analise o equilíbrio em B; depois, usando o resultado para a força em BC, anal
Duas esferas, A e B, têm massas iguais e estão eletrostaticamente carregadas, de modo que a força repulsiva que atua entre elas tem uma intensidade de 20 mN e está direcionada ao longo da linha AB. De
As molas BA e BC possuem uma rigidez de 500 N/m cada e um comprimento não esticado de 3 m. Determine o deslocamento d da corda a partir da parede quando uma força F = 175 N é aplicada à corda.
O tubo de 30 kg é suportado em A por um sistema de cinco cordas. Determine a força em cada corda para que haja equilíbrio.
Os blocos D e E possuem uma massa de 4 kg e 6 kg, respectivamente. Se x = 2 m, determine a força F e a distância s para que haja equilíbrio.