Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 72
Os membros de um suporte são conectados por um pino na junta O. Determine as intensidades de e para o equiíbrio. Considere .
Passo 1
Show de bolinhas galerinha bonita, tudo beleza com vocês? Bora lá fazer esse exercício aqui!!
Saca só, o enunciado nos deu um sistema de forças atuando sobre um suporte como no diagrama a seguir
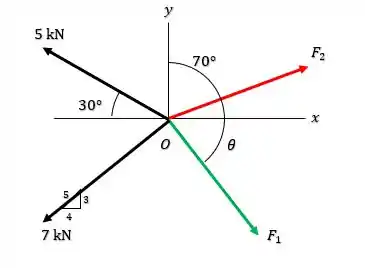
E sabendo que o sistema está em equilíbrio, o enunciado quer que a gente encontre os valores de e para satisfazer essa condição!
Passo 2
Sendo assim, podemos usar as equações do equilíbrio em cada eixo dadas como::
Adotando como sentido positivo os sentidos para a direita (eixo x) e para cima (eixo y), vamos obter que::
Logo:
Agora para o eixo :
Tal que:
Passo 3
Como temos duas equações com duas variáveis e , podemos montar um sisteminha tal que:
Resolvendo o sistema, obtemos que: