Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 7.Problemas - Ex. 56

53- O cilindro de massa m e raio r rola sem deslizar sobre a superfície circular de raio ρ . Um pequeno corpo de massa m / 4 está preso ao cilindro. Determine o máximo valor de ρ para o qual o corpo é estável na posição de equilíbrio mostrada.

Passo 1

Vamos redesenhar esse sistema com o cilindro tendo deslocado um ângulo θ em relação ao seu centro do raio da superfície onde ele está inserido.

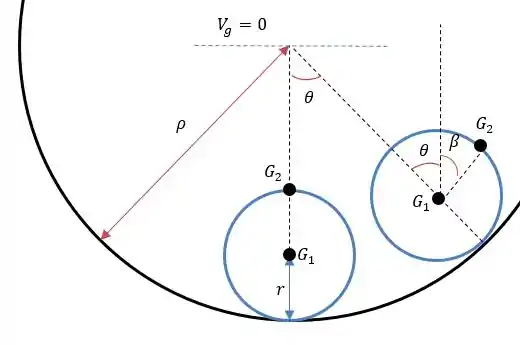
Onde se cilindro translada θ em relação ao centro do círculo e rotaciona um ângulo β em relação ao seu centro. E os dois ângulos estão relacionados ao se comparar o tamanho do arco que o raio ρ faz com o ângulo ϕ e e o tamanho que o raio r faz com o ângulo θ + β da seguinte forma:

r θ + β = ρ θ

r β = θ ( ρ - r )

β = ρ - r θ r

Passo 2

Dessa forma podemos escrever a equação da energia potencial gravitacional do sistema ao se considerar o eixo nulo no centro do círculo que forma o plano.

A altura do centro de massa G 1 será dada por:

h G 1 = - ρ - r cos ⁡ θ

Para encontrar a altura h G 2 que representa altura do centro de massa G 2 nós temos que ver a figura abaixo:

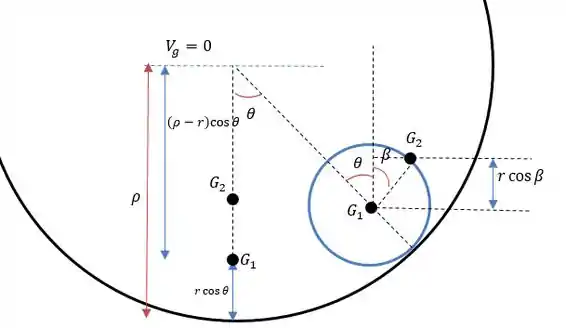
Logo a altura do centro de massa 2 será:

h G 2 = ρ - r cos ⁡ θ - r cos ⁡ β = - ρ - r cos ⁡ θ + r cos ⁡ ρ - r θ r

Passo 3

Como a massa do corpo 1 é m e a do corpo 2 é m 4 logo a energia potencial gravitacional do sistema será:

V = - m g   ρ - r cos ⁡ θ - m g 4   ρ - r cos ⁡ θ - r cos ⁡ ρ - r θ r

Arrumando essa equação teríamos:

V = - 5 4 m g ρ - r cos ⁡ θ + m g r 4 cos ⁡ ρ - r θ r

Derivando essa equação em relação a θ nós teríamos (uso da regra da cadeia):

d V d θ = + 5 4 m g ρ - r sin ⁡ θ - ρ - r r × m g r 4 sin ⁡ ρ - r θ r

d V d θ = - ρ - r 4   m g sin ⁡ ρ - r θ r + 5 4 m g ρ - r sin ⁡ θ

Derivando de novo essa equação em relação a θ :

d 2 V d θ 2 = - ρ - r 2 4 r   m g cos ⁡ ρ - r θ r + 5 4 m g ρ - r cos ⁡ θ

Passo 4

Para θ = 0 temos a seguinte condição de estabilidade:

- ρ - r 2 4 r   m g + 5 4 m g ( ρ - r ) > 0

Cortando ρ - r e m g temos:

ρ - r 4 r < 5 4

ρ - r < 5 4 ( 4 r )

ρ - r < 5 r

ρ < 6 r

Resposta

ρ < 6 r

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se  a  função de potencial de um  sistema conservativo com um grau de liberdade é  V = ( 8 x 3 - 2 x 2 - 10 ) J , onde  x é dado em metros, determine as posições de equilíbrio e investigue a estabilid
A  mola  da  balança  tem  um  comprimento  a quando  não  deformada.  Determine  o  ângulo  θ   de  equilíbrio quando o peso  W  é suportado na plataforma. Despreze  o  peso  dos  elementos. Que  val
A  haste uniforme tem 80k g de massa.  Determine  o  ângulo  θ   de  equilíbrio e investigue a sua estabilade quando estiver nessa posição A mola não está deformada quando  θ = 90 ° ?
Se  a  função de potencial de um  sistema conservativo com um grau de liberdade é  V = ( 10 cos ⁡ 2 θ + 25 sin ⁡ θ ) J , onde  0 °θ180 ° , determine as posições de equilíbrio e investigue a estabilida
A pequena balança postal consiste em um contrapeso W 1 , conectado aos elementos que possuem peso desprezível. Determine o peso W 2 que está na bandeja em termos dos ângulos θ e ϕ e das dimensões most