Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 7.Problemas - Ex. 69
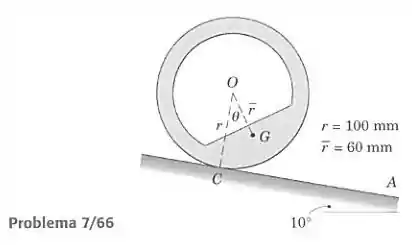
Determine os valores de equilíbrio de e a estabilidade do equilíbrio em cada posição para a roda não balanceada sobre a rampa de 10°. O atrito estático é suficiente para prevenir deslizamento. O centro de massa está em .
Passo 1
Se o sistema está em equilíbrio, ao girarmos a roda em torno de um ângulo pequeno , devemos ter uma variação da energia potencial do sistema igual a zero:
Além disso, se a segunda derivada da função potencial for positiva, o equilíbrio será estável:
Então, vamos calcular a variação da energia potencial gravitacional relacionada com , e tentar satisfazer a condição de equilíbrio estável.
Passo 2
O primeiro passo é determinar as coordenadas do centro de massa da roda. Vamos definir que o ponto de altura zero ocorre quando . Então para um giro a roda anda uma distância no plano, para cima.
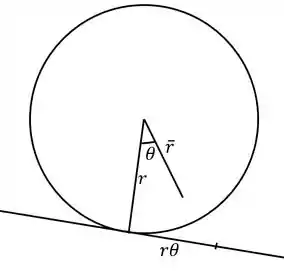
A altura do centro de massa então é:
Substituindo os valores das distâncias:
Passo 3
Agora vamos obter a expressão da variação da energia potencial gravitacional. A variação da altura do centro de massa em função e é obtida por derivação de :
Então temos a expressão de :
Queremos que a derivada da função potencial em relação a seja zero:
Então aplicamos o inverso do seno, e achamos :
Os valores obtidos são então:
Agora vamos verificar o equilíbrio estável. Derivando novamente a função, temos:
Para , temos:
Então temos um equilíbrio estável nesse caso.
Para , temos:
Então temos um equilíbrio instável nesse caso.