Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 86
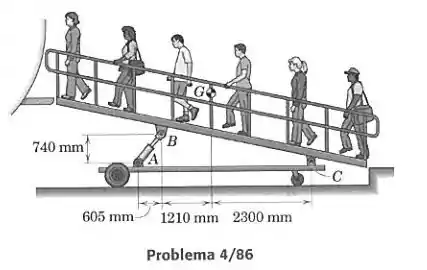
A rampa é usada para o embarque de passageiros em um pequeno avião de transporte. A massa total da rampa e de seis passageiros vale 750 kg, com centro de massa em . Determine a força no cilíndrico hidráulico AB e o módulo da reação do pino em .
Passo 1
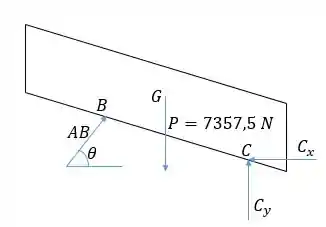
Aqui devemos considerar o conjunto total da rampa com os passageiros como um corpo só, sujeito à força peso em , à força de reação em e à força feita pelo cilindro hidráulico em . A força peso vale . Vamos representar nosso corpo em um diagrama de corpo livre:
Passo 2
A primeira coisa a fazer é encontrar o seno e o cosseno do ângulo que entrará nas nossas equações. Vamos olhar o triângulo que tem como hipotenusa. Temos:
Passo 3
Agora vamos aplicar para o corpo as três condições de equilíbrio: as equações para forças em e e uma equação de momento. Vamos fazer primeiro o momento em torno de para encontrar diretamente. A linha de ação de passa em e sua componente vertical nesse ponto vale . Então:
Substituindo pelo valor do seno calculado:
A força está comprimindo o cilindro AB.
Passo 4
Agora que só temos e como incógnitas, as encontramos com as somas das forças verticais e horizontais:
Usando os valores que já achamos nos outros passos, achamos :
Agora para encontrar :
Passo 5
Agora só falta calcular o módulo da força em :