Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas fundamentais - Ex. 10

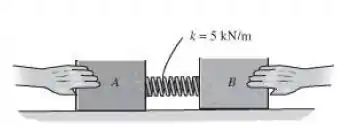
A mola está fixada ao bloco A e o bloco B é pressionado contra a mola. Se a mola está comprimida de s = 200   m m , e os blocos são liberados, determine suas velocidades no instante em que o bloco B perde contato com a mola. As massas dos blocos A e B são 10   k g e 15   k g , respectivamente.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Vamos aplicar o princípio da conservação de energia para encontrar as velocidade com que A e B são liberados.:

T 1 + V 1 = T 2 + V 2

1 2 m A v A 1 2 + 1 2 m B v B 1 2 + 1 2 k x 1 2 = 1 2 m A v A 2 2 + 1 2 m B v B 2 2 + 1 2 k x 2 2

Substituindo os valores, temos:

1 2 10 0 2 + 1 2 15 0 2 + 1 2 5 ⋅ 10 3 0,2 2 = 1 2 10 v A 2 2 + 1 2 15 v B 2 2 + 1 2 5 ⋅ 10 3 0 2

10 v A 2 2 + 15 v B 2 2 = 2 00

Passo 2

Como precisamos de outra equação para resolver o sistema, podemos aplicar a conservação de movimento linear:

  → +           m A v A 1 + m B v B 1 = m A v A 2 + m B v B 2

Substituindo os valores, temos:

  → +           10 0 + 1 5 0 = 10 v A 2 + 15 v B 2

10 v A 2 + 15 v B 2 = 0

v A 2 = - 1,5 v B 2

Agora temos duas equações para duas incógnitas, assim podemos resolver o nosso sistema:

10 - 1,5 v B 2 2 + 15 v B 2 2 = 200

v B 2 = 2,31   m / s     ( → )

v A 2 = - 1,5 2,31

v A 2 = - 3,464   m / s

v A 2 = 3,464   m / s     ( ← )

Resposta

v B 2 = 2,31   m / s     ( → )

v A 2 = 3,464   m / s     ( ← )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A bala de canhão de 5k g é disparada horizontalmente por um canhão de 250k g , como mostra a figura. Se a velocidade de saída da bala é 600m / s , medida relativamente ao solo, determine a velocidade
O bloco A tem massa de 4k g e o B tem massa de 6k g . Uma mola que tem rigidez k = 40N / m está fixada a B e comprimida de 0,3m contra A , como mostra a figura. Determine os ângulos máximos θ e ϕ dos
O bloco A de 2 0k g é rebocado para cima na rampa do carrinho de 40k g usando-se o motor M montado ao lado do carrinho. Se o motor enrola o cabo a uma velocidade constante de 5m / s , medida relativam
O guincho na traseira do jipe A é acionado e puxa o cabo de reboque a 2m / s , medidos relativamente ao jipe. Se tanto o carro B , de 1,25M g , quanto o jipe A , de 2,5M g , estão livres para se mover
O bloco A tem massa de 2k g e desliza para dentro de uma caixa com as extremidades abertas a uma velocidade de 2m / s . Se a caixa B tem massa de 3k g e está em repouso sobre a placa P , que tem massa