Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 26

A mola AB de k constante é fixada a um suporte em A e a um colar de massa m. O comprimento não alongado da mola é l . Sabendo que o colar é liberado do repouso em x = x 0 e desprezando o atrito entre o colar e a haste horizontal, determine a magnitude da velocidade do colar conforme ele passa pelo Ponto C

Passo 1

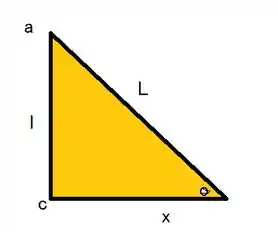
Escolha a origem no Ponto C e seja x positivo à direita. Então x é uma coordenada de posição do controle deslizante B e x0 é seu valor inicial. Seja L o comprimento esticado da mola. Então, do triângulo retângulo

L = l 2 + x 2

A elongação da mola é e = L - l e a magnitude da força exercida pela mola é:

F x = k e = k l 2 + x 2 - l

Passo 2

Pela geometria podemos fazer o somatório das forças :D

c o s ⁡ θ = x l 2 + x 2   + Σ F x = m a x : - F x c o s ⁡ θ = m a  

- k l 2 + x 2 - l x l 2 + x 2 = m a

a = - k m x - l x l 2 + x 2

∫ 0 v   v d v = ∫ x 0 1 '   a d x

Passo 3

E agora pela integral podemos determinar a expressão da velocidade

1 2 v 2 | 0 v = - k m ∫ x 0 0   x - l x l 2 + x 2 d x = - k m 1 2 x 2 - l l 2 + x 2 | x 0 0

1 2 v 2 = - k m 0 - l 2 - 1 2 x 0 2 + l l 2 + x 0 2

v 2 = k m 2 l 2 + x 0 2 - 2 l l 2 + x 0 2

= k m l 2 + x 0 2 - 2 l l 2 + x 0 2 + l 2

v = k m l 2 + x 0 2 - l

Resposta

v = k m l 2 + x 0 2 - l

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A caixa de 100 kg é içada pelo motor M . Se a velocidade da caixa aumenta uniformemente, de 1,5 m/s para 4,5 m/s em 5 segundos, determine a tração desenvolvida no cabo durante o movimento.
A balia jubarte de 5,5 Mg está encalhada na praia, devido à variação na maré. Em um esforço para resgatar a baleia, um barco rebocador de 12 Mg é utilizado para libertá-la empregando uma corda inexten
A caixa de 100 kg é içada pelo motor M . O motor excerce no cabo uma força T = 200 t 1 / 2 + 150N onde t está em segundos. Se a caixa parte do repouso no solo, determine a velocidade da caixa quando t
A força atuando sobre um projétil que tem massa m , enquanto este passa horizontalmente pelo cano do canhão é F = C sen ⁡ ( π t / t ' ) . Determine a velocidade do projétil quando t = t ' . Se o projé
A prancha rígida de 15k g é atingida pela cabeça do martelo H de 7,5k g . Imediatamente antes do impacto, o martelo é seguro livremente e tem uma velocidade vertical de 22,5m / s . Se o coeficiente de