Um trem do traslado do aeroporto viaja entre dois terminais separados por 1,6 mi. Para manter o conforto do passageiro, a aceleração do trem é limitada a ± 4ft/s², e o solavanco, ou taxa de variação da aceleração, é limitada a ± 0,8 pés/s² por segundo. Se a lançadeira tem uma velocidade máxima de 20 mi/h, determine (a) o menor tempo para a lançadeira viajar entre os dois terminais, (b) a velocidade média correspondente da lançadeira

(a) Para obter o trem, o trem deve acelerar e desacelerar na taxa máxima para maximizar o tempo para o qual v = vmax. O tempo necessário para o trem ter uma aceleração de 4 pés/s² é encontrado a partir de:

Ou

Ou

Agora,

Depois de 5s, a velocidade do trem é:

Ou

Então, como , o trem continuará a acelerar a 4 pés/s² até v = vmax. A curva a — t deve ter a forma mostrada. Observe que a magnitude da inclinação de cada porção inclinada da curva é de 0,8 pés/s²/s.

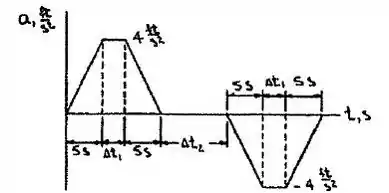
Agora:

Ou

Então

Usando simetria, a curva v—t está desenhada abaixo

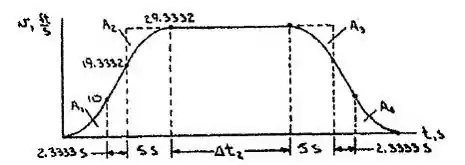
Note que , e que a áre sob a curva v---t é igual a Xmax, temos:

Ou

Então

Ou

(b) Temos

Ou