Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.3 - Ex. 8

  1. A mola de constante k não está distendida quando θ = 0 . Obtenha uma expressão para a força P necessária para defletir o sistema de um ângulo θ . A massa das barras é desprezível.

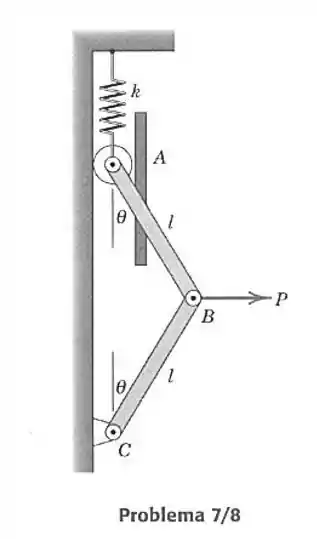
Passo 1

Quando θ = 0 a mola tem comprimento inicial y = l 0 igual a 0 , logo o comprimento de A C inicial é de 2 l .

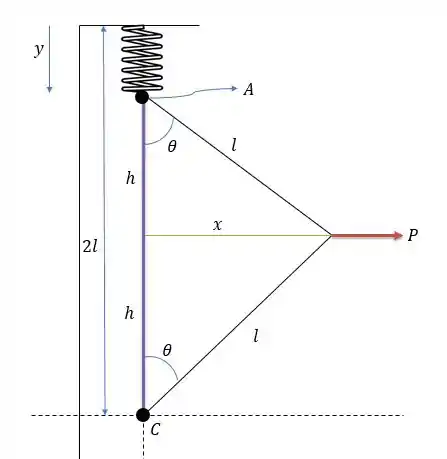
Quando θ assume um valor diferente de zero a mola passa a possuir um comprimento igual a:

l f = 2 l - 2 h

Com h valendo:

cos ⁡ θ = h l → h = l cos ⁡ θ

Logo a distorção total da mola valerá:

y = l f - l 0 = 2 l - 2 l cos ⁡ θ

O trabalho da mola faz o tamanho de y diminuir, logo o trabalho dessa mola será:

δ U y = - k 2 l - 2 l c o s   θ δ y

Onde δ y será:

δ y = δ 2 l - 2 l c o s   θ = 2 l s i n   θ   δ θ

δ U y = k 2 l - 2 l c o s   θ 2 l s i n   θ δ θ = k ( 4 l 2 sin ⁡ θ - 4 l 2 sin ⁡ θ cos ⁡ θ ) δ θ

Passo 2

O trabalho feito pela força P tende a aumentar o comprimento x , logo:

δ U P = P δ x

Onde x será calculado por:

sin ⁡ θ = x l → x = l sin ⁡ θ

Onde δ x valerá:

δ x = l cos ⁡ θ   δ θ

Passo 3

Logo a somatória dos trabalhos virtuais será:

δ U = δ U p + δ U y = P l c o s   θ   δ θ - k ( 4 l 2 sin ⁡ θ - 4 l 2 sin ⁡ θ cos ⁡ θ ) δ θ = 0

Arrumando essa equação:

P l cos ⁡ θ - 4 k l 2 ( sin ⁡ θ - sin ⁡ θ cos ⁡ θ ) = 0

P l cos ⁡ θ = 4 k l 2 ( sin ⁡ θ - s i n θ cos ⁡ θ

Dividindo os dois lados por l cos ⁡ θ :

P = 4 k l sin ⁡ θ cos ⁡ θ - sin ⁡ θ cos ⁡ θ cos ⁡ θ

P = 4 k l ( t g   θ - sin ⁡ θ )  

Resposta

P = 4 k l ( t g   θ - sin ⁡ θ )  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o problema 10.45 considerando que os operacios desceram para um ponto próximo ao solo de modo que θ = - 20 ° .
Voltando ao Problema 10.43 e usando o valor encontrado para a força exercida pelo cilindro hidráulico CD, determine a mudança no comprimento de CD necessária para se elevar a carga de 10kN em 15 mm.
Representado por μ s , o coeficiente de atrito estático entre o bloco e a barra ACE e a superfície horizontal, deduza as expressões em termos de P s ,μ s e θ para a maior e menor intensidade da força
Usando o método da Seção 10.8, resolva o Problema 10.30.
Usando o método da Seção 10.8, resolva o Problema 10.29.