Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.9 - Ex. 180

180- A água doce em um canal é contida pela placa uniforme de , que pode bascular livremente em . Se a comporta foi projetada para abrir quando a profundidade da água atingir , como mostrado na figura, qual deve ser o peso da comporta (em newtons por metro de comprimento horizontal perpendicularmente ao plano do papel)?

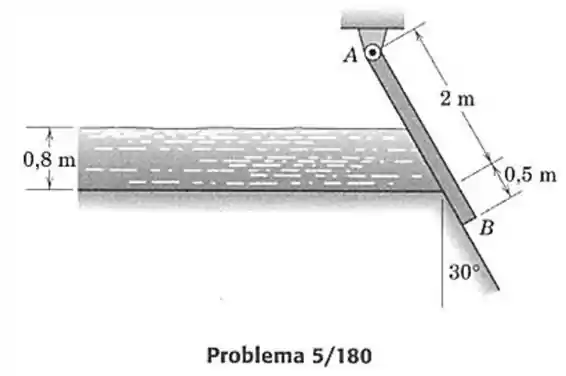
Passo 1

Vamos fazer o diagrama de forças dessa comporta de modo que a força de ação da água se encontra normal a comporta:

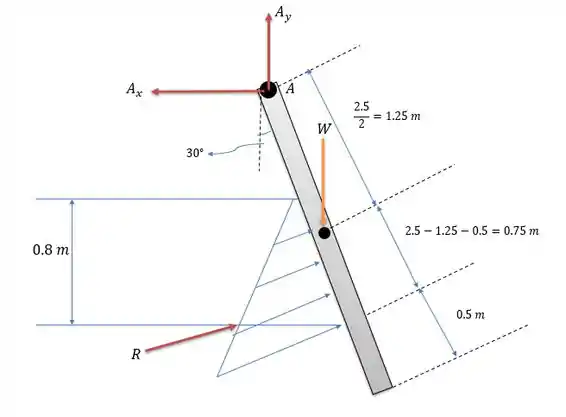
A pressão total que a água faz na comporta é a mesma caso a comporta não estivesse inclinada, que é:

Como a densidade da água doce é de a pressão será de:

Passo 2

Para calcular a força precisamos fazer a área do triângulo retângulo inclinado na figura, que terá as seguintes medidas:

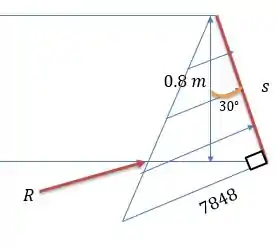
Onde o valor de valerá:

Então o valor de valerá:

E essa força estará situada em um valor na barra (como coordenadas inclinadas mesmo) igual a

Passo 3

Agora estamos aptos a descobrir o peso da comporta ao fazer a somatória dos momentos em .

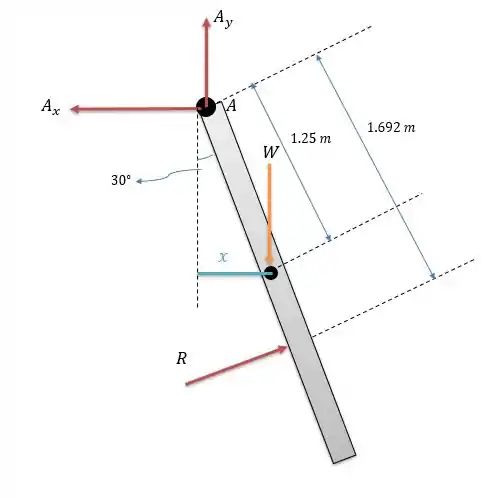
A distância horizontal de até o ponto é calculado como:

Logo a somatória dos momentos em nos dá:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

2.42. Determine a intensidade e o ângulo medido no sentido anti-horário a partir do eixo y positivo da força resultante que atua no suporte se F B = 600N e θ = 20 °

2.36. Se Φ = 30 ° e F 2 = 3k N , determine a intensidade da força resultante que atua sobre a chapa e sua direção θ, medida no sentido horário a partir do eixo x positivo.

2.41. Determine a intensidade e a direção θ de F B , de modo que a força resultante seja direcionada ao longo do eixo y positivo e tenha uma intensidade de 1500N .

2.40. Determine a intensidade e a direção, medida no sentido anti-horário a partir do eixo x positivo, da força resultante das três forças que atuam sobre o anel A. Considere F 1 = 500N e θ = 20 ° .

2.39. Determine a intensidade de F 1 e sua direção θ, de modo que a força resultante seja direcionada verticalmente para cima e tenha a intensidade de 800N .