Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 59

Usando o método da Seção 10.8, resolva o Problema 10.29.

Passo 1

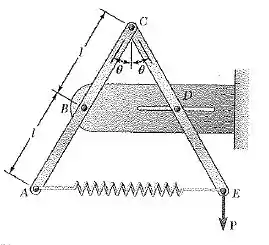
Primeiro vamos entender o problema. Temos duas hastes AC e CE que são conectados por um pino em C e por uma mola AE. Sabemos que a constante da mola é k, e a questão diz que ela não é esticada quando θ = 30 ° .

Logo, precisamos encontrar uma equação em função de P, θ , l e k para derivar satisfazendo o equilíbrio.

Passo 2

Achou um pouco complicado? Vamos destrinchar!

Observe na figura o triângulo Δ A A ' B , o ângulo θ é entre a hipotenusa AB e o cateto A’B. Desse modo:

cos ⁡ θ = A ' B A B

Assumindo que, l = A B e que y e = A ' B , temos:

y e = l c o s   θ

Agora observe na figura o triângulo Δ A E C , obtemos que:

sin ⁡ θ = A E / 2 2 l = A E 4 l

Assumindo que, x = A E , temos:

x = 4 l s i n   θ

Para o comprimento não esticado teremos:

x 0 = 4 l s i n   30 ° = 2 l

Passo 3

Agora vamos analisar a deflexão da mola. Sabemos que:

s = x - x 0

Substituindo:

s = 4 l sin ⁡ θ - 2 l

s = 2 l ( 2 sin ⁡ θ - 1 )

Pela energia potencial, temos que:

V = 1 2 k s 2 + P y e

Substituindo:

V = 1 2 k 2 l 2 sin ⁡ θ - 1 2 + P ( - l c o s   θ )

Derivando e igualando a 0, teremos:

d V d θ = 4 k l 2 2 sin ⁡ θ - 1 2 cos ⁡ θ + P l s i n   θ = 0

Simplificando:

2 sin ⁡ θ - 1 cos ⁡ θ sin ⁡ θ + P 8 k l = 0

Portanto:

P 8 k l = 1 - 2 sin ⁡ θ tan ⁡ θ

Resposta

P 8 k l = 1 - 2 sin ⁡ θ tan ⁡ θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A ponte de 2 Mg, com centro de massa no ponto G, é levantada pelas duas vigas CD, localizadas em cada lado da ponte. Se o contrapeso E de 2 Mg estiver conectado às vigas como mostrado, determine o âng
O mecanismo conectado por pinos é restringido por um pino em A e um rolete em B. Determine a força P que deve ser aplicada ao rolete para manter o mecanismo em equilíbrio quando θ = 30 º º. A mola est
5. Determine o ângulo θ onde a barra de 50k g está em equilíbrio. A mola está livre em θ = 60 ° .
4. O mecanismo está sujeito a uma força P = 6k N . Determine o ângulo θ para o equilíbrio. A mola está livre em θ = 60 ° . Despreze a massa dos membros.
13. Determine os ângulos θ para equilíbrio do disco de 20N ( ≈ 2k g ) usando o princípio do trabalho virtual. Despreze o peso da barra. A mola está livre quando θ = 0 ° e sempre permanece na vertical