Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 48

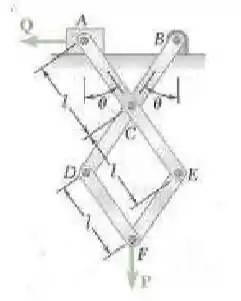
Representado por μ s , o coeficiente de atrito estático entre o bloco e a barra ACE e a superfície horizontal, deduza as expressões em termos de P s ,   μ s e θ para a maior e menor intensidade da força Q para as quais o equilíbrio é mantido.

Passo 1

Hey hey galerinha! Vamos pra essa questão tranquilos, o segredo dela está na gente montar a equação para o momento! Observando os nós e o bloco de massa fixa, temos que para a equação de equilíbrio do momento:

- x A + x A 2 P = 0

Logo,

F = μ s A = μ s P 2 = 1 2 μ s P  

Passo 2

Pegaram a ideia? Agora vamos partir para a dedução das equações para o tranalho virtual.

Temos que:

x A = 2 s e n θ

d x A = 2 c o s θ d θ

Tambem:

y F = 3 c o s θ

d y F = - 3 s e n θ d θ

Passo 3

Vamos passar agora para o nosso trabalho virtual, já que temos os nossos valores para y F e x A e suas respectivas diferenciações.

d U = 0

Q m á x - F d x A + P d y F = 0

Q m á x - 1 2 μ s P   2 c o s θ d θ - P 3 s e n θ d θ = 0

Q m á x = 3 2 P t a n θ + 1 2 μ s P

Simplificando, o nosso Q m á x , temos que:

Q m á x = P 2 ( 3 t a n θ + μ s )

Agora para o Q m i n , temos que para a força ser mínima, significa que o coeficiente de atrito atua para a esquerda, ou seja, trocamos μ s por - μ s e encontramos:

Q m i n   = P 2 ( 3 t a n θ - μ s )

Resposta

Q m á x = P 2 ( 3 t a n θ + μ s ) e Q m i n   = P 2 ( 3 t a n θ - μ s )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma “caixa preta” contém uma série de cremalheiras e pinhões, engrenagens e outros elementos mecânicos internos interconectados, os quais transformam o movimento linear da haste A em um movimento line
A barra leve O C é articulada em O e balança no plano vertical. Quando θ = 0 , a mola de rigidez k não está alongada. Determine o ângulo de equilíbrio, correspondente a uma força vertical P aplicada à
Identifique quais dos itens de ( a ) até ( f ) são mais bem resolvidos ( A ) pelas equações de equilíbrio de força e momento e ( B ) por trabalho virtual. Descreva sucintamente o procedimento para cad
A figura mostra a seção transversal de um recipiente composto por uma casca hemisférica de raio r e uma casca cilíndrica de altura h , feitas do mesmo material. Especifique o limite de h para haver es
A casca semicilíndrica de raio r gira em torno de um eixo, pelos pontos O , como mostrado. A massa das duas hastes de suporte é pequena comparada à massa da casca. Determine o valor máximo de h para o