Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.3 - Ex. 6
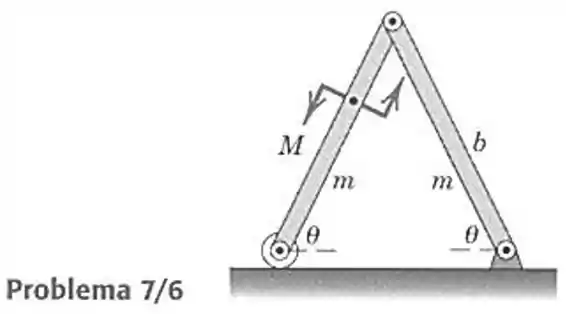
- Cada uma das conexões uniformes do conjunto tem massa e comprimento . A posição de equilíbrio do conjunto, no plano vertical, é determinada pelo binário , aplicado a conexão da esquerda. Expresse em função de .
Passo 1
O binário de forças pode ser visto como um momento (no caso para o sentido anti-horário) o que faz aumentar o ângulo , logo o trabalho pode ser calculado por:
Agora o sistema de forças causado pelas barras podem ser vistos como:
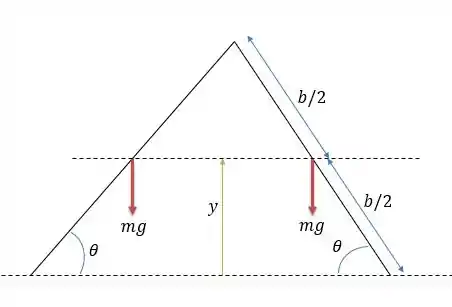
Os trabalhos feitos pelas forças da barra fazem diminuir a linha , logo o trabalho virtual será:
Logo a somatória dos trabalhos virtuais desse sistema será:
Passo 2
O comprimento pode ser encontrado ao fazer o seno de .
Logo a somatória dos trabalhos virtuais será:
Fazendo essa derivada temos:
Isolando o cosseno e cortando temos:
Resposta
Exercícios de Livros Relacionados
Sabendo que o coeficiente de atrito estático entre o colar C e a haste vertical é 0,40 , determine a intensidade do maior e do menor binário M para o qual equilíbrio é mantido na posição mostrada quan
Um bloco de peso W é levado ao repouso em um plano formando um ângulo α com a horizontal por meio de uma força P direcionada ao longo do plano. Se μ é o coeficiente de atrito entre o bloco e oplano de
Usando o método do trabalho virtual, determine a reação em E.
Determine o movimento vertical do nó D se o comprimento do elemento BF é aumentado em 1.5 in.(Dica: aplique uma carga vertical no nó D e, usando os métodos do Capítulo 6, calcule a força exercida pelo
Sabendo que o coeficiente de atrito estático entre o bloco preso à barra ACE e a superfície horizontal é igual a 0,15 , determine as intensidades da maior e da menor força Q para as quais o equilíbrio