Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 36

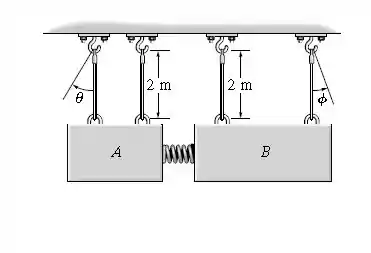
O bloco A tem massa de 4   k g e o B tem massa de 6   k g . Uma mola que tem rigidez k = 40   N / m está fixada a B e comprimida de 0,3   m contra A , como mostra a figura. Determine os ângulos máximos θ e ϕ dos cabos após os blocos serem liberados do repouso e a mola tornar-se não deformada.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Podemos aplicar conservação de quantidade de movimento para encontrar a velocidade do sistema após a colisão:

→ +         ∑ m v 1 = ∑ m v 2

→ +         m A v A 1 + m B v B 1 = m A v A 2 + m B v B 2

Substituindo os valores, temos:

→ +         4 0 + 6 0 = 4 - v A 2 + 6 v B 2

v A 2 = 1,5 v B 2

Passo 2

Aplicando o principio da conservação de energia para quando os blocos são liberados, temos:

T 1 + V 1 = T 2 + V 2

1 2   m A v A 1 2 + 1 2 m B v B 1 2 + 1 2 k s 1 2 = 1 2 m A v A 2 2 + 1 2 m B v B 2 2 + 1 2 k s 2 2

1 2 4 0 2 + 1 2 6 0 2 + 1 2 4 0 0,3 2 = 1 2 4 v A 2 2 + 1 2 5 v B 2 2 + 1 2 4 0 0 2

3,6 = 4 v A 2 2 + 6 v B 2 2

Substituindo a informação encontrada no passo 1, temos:

3,6 = 4 1,5 v B 2 2 + 6 v B 2 2

v B 2 = 0,49   m / s

v A 2 = 0,735   m / s

Vamos analisar o bloco A tomando como referência o ponto mais baixo:

T 1 + V 1 = T 2 + V 2

1 2 4 0,735 2 + 0 = 0 + 4 9,81 ( 2 ) ( 1 - cos ⁡ θ )

Resolvendo a equação acima temos:

θ = 9,52 °

Para B , temos:

1 2 6 0 , 49 2 + 0 = 0 + 6 9,81 ( 2 ) ( 1 - cos ⁡ ϕ )

ϕ = 6,34 °

Resposta

θ = 9,52 °

ϕ = 6,34 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bloco A de 10k g é liberado do repouso 2m acima da placa P de 5k g , que pode deslizar livremente sobre as guias verticais lisas B C e D E . Determine a velocidade do bloco e da placa logo após o i
O caminhão de 5M g e o carro de 2M g estão viajando nas velocidades mostradas imediatamente antes de colidirem. Após a colisão o carro move-se com uma velocidade de 15k m / h para a direita em relação
A bola de 2k g é lançada de modo a se mover horizontalmente a 10m / s quando atinge o bloco de 6k g , que está descendo o plano inclinado a 1m / s . Se o coeficiente de restituição entre a bola e o bl
A bola de 2k g é lançada de modo a se mover horizontalmente a 10m / s quando atinge o bloco de 6k g , que está descendo o plano inclinado a 1m / s . Se o coeficiente de restituição entre a bola e o bl
Dois carros A e B têm massa de 2000k g e colidem no pavimento escorregadio de um cruzamento. A direção do movimento de carro após a colisão é medida pelos rastros deixados, como mostrado. Se o motoris