Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 60
Uma mola, tendo um comprimento não deformado de , temo uma bola de presa em uma extremidade. Determine o ângulo da mola se a bola tem uma velocidade de tangente à trajetória circular horizontal.
Passo 1
A chave de problemas de cinética está no diagrama de corpo livre. Ao identificarmos todas as forças que o nosso problema está sujeito, conseguiremos visualizar o que há de ser feito mais facilmente.
Relembrando do capítulo de cinemática, vimos que a aceleração centrípeta de um corpo é dada por:
Relembrando também como se calcula a força elástica de uma mola, temos que o seu valor é dado pelo produto da sua constante elástica pela sua deformação, isto é
Vamos a questão então!
Passo 2
Vamos começar por esboçar o diagrama de corpo livre do nosso problema. Desta forma, a bola está sujeita a:
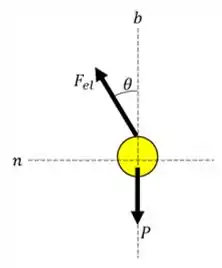
Temos apenas a presença da força peso e da força elástica na nossa bola.
Passo 3
Na direção do eixo , perpendicular ao plano dado pelas direções tangencial e normal, a bola não está sujeita a nenhuma aceleração. Portanto,
Temos que determinar uma outra equação que relacione os valores de e para podermos resolver um sistema. Para isto, vamos analisar agora as forças na direção normal.
Passo 4
Fazendo o somatório das forças na direção normal, obtemos:
Opa, chegamos a um impasse. Quem é esse que aparece na equação acima?
Se lembrarmos da componente normal da aceleração, lembramos que ela é o raio da trajetória. Hum, já temos uma informação. E como obtemos ele??? Para isto, precisamos observar a geometria do nosso problema. Ele nos diz que:
Portanto, temos:
Esta é uma equação difícil de se resolver analiticamente. Utilizando ferramentas computacionais, descobrimos que . Com este valor voltamos para calcular o comprimento final da mola. Portanto, obtemos: