Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 102

Um brinquedo do parque de diversões gira com uma velocidade angular constante de θ ˙ = 0,8   r a d / s . Se a trajetória do brinquedo é definida por r = ( 3 sen ⁡ θ + 5 )   m e z = ( 3 cos ⁡ θ ) m , determine as componentes da força r , θ e z exercidos pelo assento sobre o garoto de 20 kg quando θ = 120 ° .

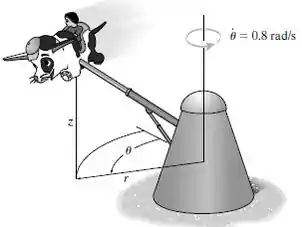
Passo 1

O Problema nos deu as seguintes informações:

Massa do menino: m = 20   k g

Velocidade angular constante: θ ˙ = 0,8   r a d / s

A questão pede para determinarmos as componentes da força exercida pelo assento sobre o garoto quando θ = 120 ° .

Desenhamos o seguinte diagrama de corpo livre:

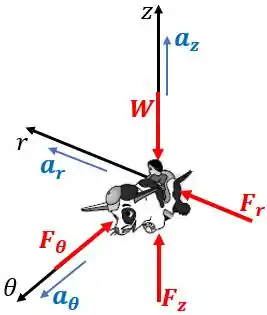
Onde W = m g é a força peso e g = 9,81   m / s 2 ;

Passo 2

Sabemos que a trajetória é definida por

r = 3 sen ⁡ θ + 5

z = 3 cos ⁡ θ

Portanto, as derivadas temporais em r são:

r ˙ = d r d t = 3 θ ˙ cos ⁡ θ   m / s

r ¨ = d 2 r d t 2 = - 3 θ ˙ 2 sen ⁡ θ + 3 θ ¨ cos ⁡ θ   m / s 2

As derivadas temporais em z são:

z ˙ = d z d t = - 3 θ ˙ sen ⁡ θ   m / s

z ¨ = d 2 z d t 2 = - 3 θ ˙ 2 cos ⁡ θ + 3 θ ¨ sen ⁡ θ   m / s 2

Como a velocidade angular θ ˙ = 0,8   r a d / s é constante, temos que θ ¨ = 0   r a d / s 2 .

Para   θ = 120 ° :

r = 7,598   m

r ˙ = d r d t = - 1,20   m / s

r ¨ = d 2 r d t 2 = - 1,663   m / s 2

z = - 1,5   m

z ˙ = d z d t = - 2,09   m / s

z ¨ = d 2 z d t 2 = 0,96   m / s 2

Passo 3

Sabemos que as componentes da aceleração nas coordenadas r e θ são dadas por

a r = r ¨ - r θ ˙ 2

a θ = r θ ¨ + 2 r ˙ θ ˙

a z = z ¨

Logo,

a r = - 0,6 ( 0,5 2 ) = - 6,526   m / s 2

a θ = + 2 - 0,15 0,5 = - 1,92   m / s 2

a z = 0,96   m / s 2

Passo 4

Aplicaremos as Equações do Movimento.

Analisando no eixo r , temos que

∑ F r = m a r

F r = m a r

F r = 20 - 6,526

F r = - 130,5 N

Analisando no eixo θ , temos que

∑ F θ = m a θ

F θ = m a θ

F θ = 20 ( - 1,92 )

F θ = - 38,4 N

Analisando no eixo θ , temos que

∑ F z = m a z

F z - W = m a z

F z = 20 0,96 + 20 ( 9,81 )

F z = 215,4 N

O sinal negativo de F r e F θ indicam que estas forças estão agindo na mesma direção, porém no sentido contrário ao desenhado no diagrama de corpo livre.

Resposta

F r = - 131 N

F θ = - 38,4 N

F z = 215 N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A sonda Viking aproxima-se do planeta Marte em uma trajetória parabólica, como mostrado. Quando ele alcança o ponto A , sua velocidade é de 10 Mm/h. Determine r 0 e a velocidade necessária em A de man
O satélite está em uma órbita elíptica em torno da Terra, como mostrado. Determine a sua velocidade vetorial no perigeu P e apogeu A , e o período do satélite.
Uma bola de massa de 1 kg e está confinada a se mover ao longo da ranhura vertical lisa devido à rotação do braço liso O A . Determine a força do braço sobre a bola e a força normal da ranhura sobre a
O ônibus espacial é lançado com uma velocidade vetorial de 28000 km/h paralela à tangente da superfície da Terra no ponto P e então se move em torno da órbita elíptica. Quando ele chega ao ponto A , s
O satélite está se movendo em uma órbita elíptica com uma excentricidade e = 0,25 . Determine a sua velocidade escalar quando ele está na sua distância máxima A e distância mínima B .