Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.7 - Ex. 162
As molas estão sem deformação na posição indicada. Se o cursor de é liberado a partir do repouso na posição em que a mola inferior é comprimida de , determine a compressão máxima da mola superior.
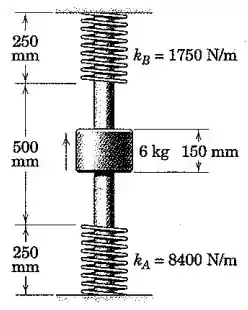
Passo 1
Pela conservação da energia mecânica, temos:
Estamos partindo do repouso e voltando ao repouso, na compressão máxima. Então . Também teremos:
De forma que a equação de conservação de energia será:
Passo 2
Agora tentaremos expressar em termos de . Se é a distância onde “não há” mola, e é o comprimento vertical do cursor, então teremos:
Passo 3
Então, retornando à equação de conservação da energia, podemos substituir os valores:
Resolvendo a equação do segundo grau acima, e desprezando a solução negativa, obtemos:
Resposta
Exercícios de Livros Relacionados
No instante mostrado, o ponto P no cabo tem uma velocidade de v P = 12m / s , que está aumentando a uma taxa de a P = 6m / s 2 . Determine a potência de entrada do motor M neste instante se ele opera
Se a superfície de contato entre o bloco de 20 kg e o solo é lisa, determine a potência de força F quando t = 4 s. Inicialmente, o bloco está em repouso.
Se F = 10 sN , onde s é dado em metros e a superfície de contato entre o bloco e o solo é lisa, determine a potência de força F quando s = 5 m. Inicialmente, o bloco de 20 kg está em repouso.
Se a carga de 50 kg A é içada pelo motor M de maneira que a carga tenha uma velocidade constante de 1,5 m/s, determine a potência de entrada do motor, o qual opera com uma eficiência de ϵ = 0,8 .
Se o motor recolhe o cabo com uma velocidade constante de v = 1 m/s, determine a potência fornecida ao motor. A carga pesa 500 N e a eficiência do motor é ϵ = 0,8 . Despreze a massa das polias.