Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.7 - Ex. 165
Um satélite é colocado em uma órbita elíptica em torno da Terra e tem uma velocidade na posição do perigeu . Determine a expressão para a velocidade na posição do apogeu . Os raios para e são, respectivamente, e . Observe que a energia total permanece constante.
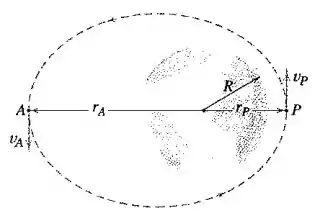
Passo 1
A conservação da energia mecânica nos dá a seguinte equação:
Lembre-se que a energia potencial gravitacional nesse caso pode ser dada por:
Então:
Passo 2
Multiplicando toda a equação anterior por e dividindo por , obtemos:
Resposta
Exercícios de Livros Relacionados
No instante mostrado, a barra de 25k g gira no sentido horário a 2r a d / s . A mola fixada em sua extremidade permanece sempre vertical, devido ao rolete guia em C . Se a mola tem um comprimento não
O sistema consiste de dois blocos, A e B , de 30 e 10k g , respectivamente, e das polias de 2,5k g C e D , que podem ser tratadas como dois discos finos. Determine a velocidade do bloco A após o bloco
Uma corrente de massa desprezível está encaixada na engrenagem, que tem massa de 2k g e raio de giração k O = 50m m . Se o bloco de 4k g A é solto do repouso a partir da posição s = 1m , determine a v
O pêndulo consiste de uma barra B A , de 2k g , e um disco de 3k g . A mola está deformada 0,09m quando a barra está na horizontal, como mostrado. Se o pêndulo é solto do repouso e gira em torno do po
O para-choque de mola dupla é usado para parar o lingote de aço de 750 kg em uma laminadora. Determine o deslocamento máximo da placa A se o lingote bate na placa com uma velocidade de 2,4 m/s. Despre