Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas Revisão - Ex. 203
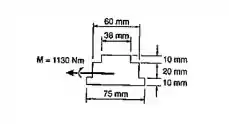
Um momento M atua em um plano vertical e é aplicado a uma viga que tem a seção transversal mostrada. Sabendo-se que E = 200 GPa, determinar as máximas tensões de tração e de compressão e o raio de curvatura da viga.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para analisarmos a figura e dizermos qual deveria ser a tensão de tração, a de compressão e o raio. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser dividir a nossa viga em 3 retângulos e montar a nossa tabelinha dos valores.
Passo 3
Pronto!! Agora é só fazermos umas matemágicas aí pra achar o resultado!!
Resposta
Exercícios de Livros Relacionados
Pede-se: (a) Mostrar que a tensão em um canto A de um membro retangular será nula, se a força vertical P for aplicada num ponto localizado sobre a linha x b / 6 + z h / 6 = 1 (b) Mostrar também que se
Em uma dada seção de um perfil laminado de aço S 200 × 34 , o efeito da gravidade é representado por um vetor-momento M 0 , Expressando por σ 0 a máxima tensão na viga quando θ = 0 , determinar o ângu
Uma viga de seção transversal assimétrica está submetida a um momento M z atuando em um plano vertical. Mostre que a tensão no ponto A de coordenadas y e z , é: σ A = - y I y - z I y z I y I z - I y z
Mostrar que: (a) Se uma força vertical P é aplicada no ponto A da seção mostrada, a equação do eixo neutro B D é x A k z 2 x + z A k x 2 z = - 1 Onde k z e k x , expressam os raios de giração da seção
Para que seja possível a entrada no interior de um tubo de seção quadrada de 6,35 m m de espessura, a porção B D de um dos lados do tubo foi removida. Sabendo-se que o carregamento no tubo é equivalen