Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 105
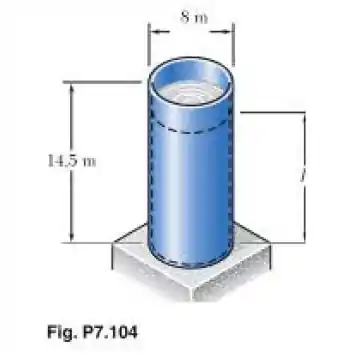
Para o tanque de armazenagem do Problema 7.104, determine a tensão normal máxima e a tensão de cisalhamento máxima na parede cilíndrica quando o tanque estiver totalmente cheio (h = 14,5 m).
Passo 1
Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, vamos precisar da equação para a tensão tangencial para um vaso cilíndrico, já que a água irá exercer essa pressão nas paredes do reservatório. Então, como vimos na equação 7.30, temos:
Em que é a pressão manométrica do vaso, é seu raio interno e a espessura do vaso. Essa será a tensão real a qual o reservatório estará submetido. No nosso caso, para encontrar a pressão exercida no vaso, vamos utilizar a equação que nos dá a pressão manométrica de um fluido com base na altura de sua coluna de líquido, que é dada por:
Feito isso, temos os valores para substituir na equação da tensão. Depois disso, para a tensão de cisalhamento máxima, vamos utilizar a equação 7,34, que nos dá:
Então bora lá!
Passo 2
Então, como vimos no passo 1, vamos encontrar a tensão a qual o reservatório está submetido através de:
Sendo assim, precisamos calcular o valor do raio interno, que é dado por:
Agora vamos calcular a pressão exercida pela coluna de água, através de:
Agora, substituindo os valores conhecidos na equação da tensão, teremos:
Essa é a tensão máxima a qual o nosso reservatório está submetido.
Passo 3
Agora ficou fácil para encontrar a tensão de cisalhamento máxima, que será dada por:
Substituindo o valor da tensão encontrada no passo 2, chegamos em:
Essa é a nossa tensão de cisalhamento máxima!! Acabamos mais um!!