Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 147

A caixa de tamanho desprezível está deslizando para baixo ao longo de uma trajetória curva definida pela parábola . Quando ela está em , a velocidade escalar é e o aumento na velocidade escalar é . Determine a intensidade da aceleração da caixa nesse instante.

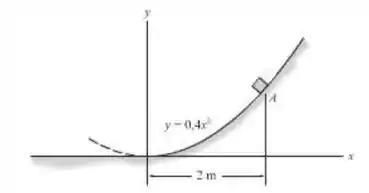
Passo 1

Precisamos determinar a intensidade da aceleração. Como já nos foi dado a sua componente tangencial, só precisamos calcular a sua componente normal. Mas aí a gente se questiona: e cadê o raio de curvatura? Este é o ponto mais difícil da questão. Para calcularmos o raio de curvatura, será necessário utilizarmos a seguinte equação:

Obtido a função para o raio da curvatura, basta substituir o valor de que obtemos o raio. Depois disto, basta utilizar as equações da cinemática para determinarmos a aceleração.

Passo 2

Antes de calcularmos a componente normal, precisamos determinar o raio de curvatura. Para isto, utilizaremos a fórmula do Passo 1. Primeiramente, derivaremos a função que governa a nossa curva duas vezes. Sendo assim:

Substituindo na fórmula do raio de curvatura, temos:

Quando , temos:

Passo 3

Agora, para calcularmos as componentes da aceleração, podemos substituir os valores diretamente nas suas equações. Como o termo tangencial já foi dado e é igual a , calcularemos a componente normal. Sendo assim, temos:

Portanto, calculando a intensidade da aceleração, temos:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O avião no parque de diversões move-se ao longo de uma trajetória definida pelas equações r = 4m , θ = 0,2 tr a d e z = 0,5 cos ⁡ θ m , onde t é dado em segundos. Determine as componentes cilíndricas

Quando θ = 15 ° o carro tem uma velocidade escalar de 50m / s a qual está aumentando a 6m / s 2 . Determine a velocidade angular da câmera acompanhando o carro nesse instante.

Um carro move-se ao longo de uma estrada, a qual, por uma curta distância, é definida por r = 60 / θm , onde θ é dado em radianos. Se ele mantém uma velocidade escalar constante de v = 10,5m / s , det

Resolva o Problema 12.188 se a came tiver uma aceleração angular de θ ¨ = 2r a d / s 2 quando sua velocidade angular é θ ˙ = 4r a d / s em θ = 30 ° .

A fenda do braço A B impulsiona o pino C pela fenda espiral descrita pela equação r = a θ . Se a velocidade angular é constante em θ ˙ , determine as componentes radiais e transversais da velocidade e