Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 86

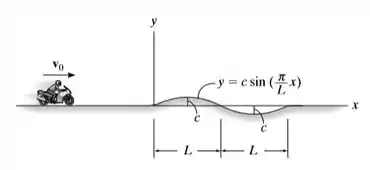
Um motociclista se move com uma velocidade escalar vd constante ao longo de uma trajetória. Onde em um pequeno trecho assume uma forma de curva senoidal. Determinar as componentes x e y da velocidade, em qualquer instante sobre a curva.

Passo 1

Como temos a função que nos dá a posição do motociclista ao longo da curva, podemos derivá-la e encontrar a função da sua velocidade sobre a curva, assim sendo:

y = c . s i n ( π L * x )

Derivando

y ' = π L c . c o s ( π L * x ) x '

Então

v y = π L c . c o s ( π L * x ) v x

Passo 2

Sabendo que a intensidade da velocidade é dada pela rais quadrada da soma dos quadrados de suas componentes, então:

v 2 = v x 2 + v y ²

Logo:

v 2 = v x 2 + ( π L c . c o s π L * x v x ) ²

v 2 = v x 2 * 1 + π L c 2 * c o s ² π L * x

Passo 3

Tendo isso, podemos assim, determinar as funções que nos dão as intensidades da velocidade em x e y, apenas rearranjando a equação. Logo:

v x = v ² 1 + π L c 2 * c o s ² π L * x

E,

  v y = π L c . c o s π L * x * v 2 1 + π L c 2 * c o s 2 π L * x

Então

v y = v * π L c . c o s π L * x 1 + π L c 2 * c o s 2 π L * x

Resposta

As intensidades das componentes da velocidade em x e em y, em qualquer momento sobre a curva, são dados por:

v x = v ² 1 + π L c 2 * c o s ² π L * x

v y = v * π L c . c o s π L * x 1 + π L c 2 * c o s 2 π L * x

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

14.47. Duas pequenas esferas A e B, de massas 2,5 kg e 1 kg, respectivamente, estão unidas por uma barra rígida de massa desprezível. As duas esferas estão em repouso sobre uma superfície horizontal s
14.50. Resolver o Problema 14.49, considerando que 45°.
14.48. Resolva o Problema 14.47, considerando que B é a esfera que é subitamente impulsionada com velocidade v0 (3 m/s)i.
14.51. Dois pequenos discos A e B de massas de 3 kg e 1,5 kg, respectivamente, podem deslizar livremente sobre uma superfície horizontal sem atrito. Os discos estão unidos por uma corda de 600 mm de c
Um jato de água de seção transversal A e velocidade v1 atinge uma placa que é mantida pela força P. Determine a intensidade de P, sabendo que A =500m m 2 , v 1 = 25 m s eV = 0 .