Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 195
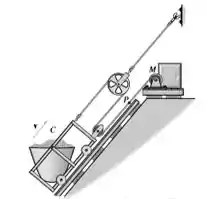
O carrinho de mineração C é puxado pelo motor M através de um conjunto de cordas e polias. Determinar a velocidade do ponto P de tal maneira que a velocidade escalar de C seja .
Passo 1
Este problema traz o conceito de polias e para resolvê-lo é importante ter em mente que existem duas cordas distintas no problema: A corda que segura a polia à parede e a corda que liga o carrinho ao motor.
Beleza, e como vamos resolver esse problema?
Vamos trabalhar em cima da velocidade da corda que liga o motor no carrinho , lembrando que numa mesma corda a velocidade de todos os pontos é igual (em módulo) podendo variar a direção.
Uma forma bem simples de fazer isso é perceber que a corda está dobrada em três partes, todas conectadas à , logo quando puxamos com uma velocidade essa velocidade será dividida por três porque a corda é inextensível.
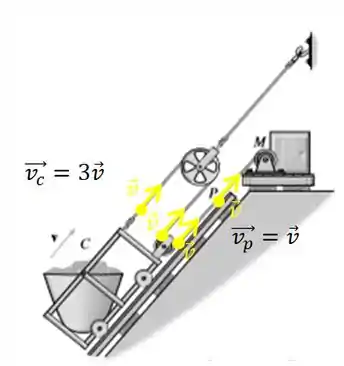
Assim .
Porém podemos fazer de uma maneira mais formal, como demonstrado abaixo.
Passo 2
Verificando apenas o conjunto de cordas e polias envolvidas no sistema, temos que:
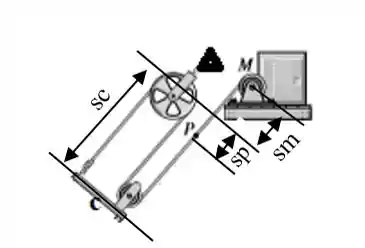
Sabendo que a corda que segura a polia superior não influencia no movimento do carro por estar ali apenas para fixar a polia, ela pode ser considerada como um ponto fixo e descartada dos cálculos. Logo o comprimento total da corda será:
Passo 3
Mas a gente não quer trabalhar com velocidade ao invés de comprimento? Então é só derivar essa equação em função do tempo, já que a derivada da posição pelo tempo é a velocidade:
Derivando a equação:
E olhando para essa derivada, vemos que será constante, afinal a posição do motor não vai se alterar, assim como o comprimento da corda , como ela é inextensível, esse comprimento não varia.
Sendo assim, teremos:
Substituindo o valor de vc=2m/s
Resposta
Para que o carrinho C tenha uma velocidade escalar constante de 2m/s, o ponto P precisa se mover a uma velocidade 3 vezes maior, ou seja, 6m/s. O que implica que o motor M deve puxar a corda a uma velocidade de 6m/s.