Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 14.Problemas - Ex. 48

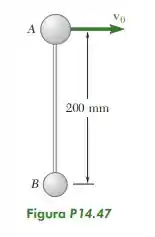
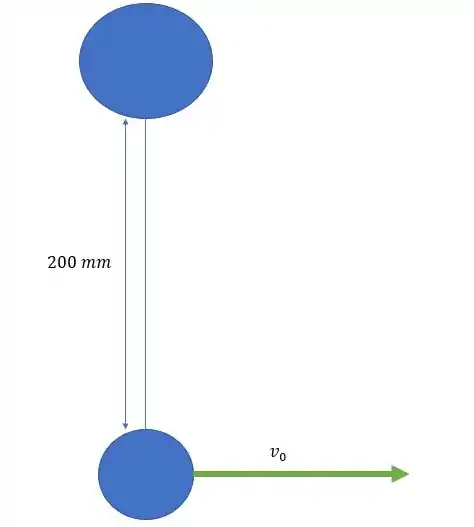
14.48. Resolva o Problema 14.47, considerando que B é a esfera que é subitamente impulsionada com velocidade v0 (3 m/s)i.

Passo 1

Vamos lá! Temos o seguinte:

A gente sabe que A B - = 200   m m , se a gente imaginar que existe um ponto G que está no centro de massa, podemos fazer

A G - + B G - = 200   m m

A esfera A tem massa de 2,5   k g e a esfera B tem massa de 1   k g , a barra rígida tem massa desprezível, então podemos fazer:

A G - → 2,5   k g

B G - → 1   k g

B G - ⋅ 1 = A G - ⋅ 2,5

E

3,5   A G - = 200

Então

A G - = 57,14   m m

B G - = 142,86   m m

Passo 2

No começo, quando a massa A é impulsionada, o momento do sistema é

L i = m B v 0

L i = 1 ⋅ 3   i ^ = 3   i ^ J

E o momento angular inicial em relação ao centro de massa é

H G = G B - × m B v 0 = - 142,86   j ^ × 3   i ^

Então

H G = 428,58   k ^   m ⋅ k g ⋅ s

Passo 3

Depois disso acontece a rotação de 180°. Agora podemos usar conservação de momento linear

L i = m A v A ' + m B v B '

3 = 2,5 ⋅ v A ' + 1 ⋅ v B '

Então

2,5 v A ' + v B ' = 3

Agora podemos usar conservação de momento em relação ao novo centro de massa.

H G = r A m A v A ' - r B m B v B '

428,58   = 57,14 2,5 v A ' - 142,86 1 v B '

Então

142,85   v A ' - 142,86   v B ' = 428,58  

Agora temos duas equações e duas incógnitas. Bom, de acordo com a equação do momento linear temos

v B ' = 3 - 2,5   v A '

Vamos substituir isso na segunda equação

142,85   v A ' - 142,86   ( 3 - 2,5   v A ' ) = 428,58  

- 214,3   v A ' - 428,58 = 428,58  

Logo

v A ' = - 4   m / s

Então

v B ' = 3 - 2,5 - 4 = 13 m s

Resposta

a : L i = 3   i ^ J ;   H G = 428,58     k ^   m ⋅ k g ⋅ s b :   v A ' = - 4 m s ;   v B ' = 13 m s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Três pequenas esferas idênticas A, B e C, que podem deslizar livremente sobre uma superfície horizontal sem atrito, estão ligadas por três fios de comprimento 200 mm que estão amarrados a um anel G. I
Três pequenas esferas idênticas A, B e C, que podem deslizar livremente sobre uma superfície horizontal sem atrito, estão ligadas por três fios de comprimento l que estão amarrados a um anel G. Inicia
Resolva o Problema 14.87 considerando que a corrente é abaixada até o solo com uma velocidade constante v .
No experimento de dispersão de partículas feito no Problema 14.24, sabe-se que a partícula alfa é lançada a partir de A 0( 300 ,0 ,300 ) e que ela colide com o núcleo de oxigênio C em Q( 240 ,200 ,100
Uma corrente de comprimento l e massa m está apoiada sobre o solo. Se sua extremidade A é erguida verticalmente a uma velocidade constante v , expresse, em termos do comprimento y da porção de corrent