Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 14.Problemas - Ex. 51

14.51. Dois pequenos discos A e B de massas de 3 kg e 1,5 kg, respectivamente, podem deslizar livremente sobre uma superfície horizontal sem atrito. Os discos estão unidos por uma corda de 600 mm de comprimento e giram no sentido anti-horário em torno do seu centro de massa G a uma taxa de 10 rad /s. No instante t 0, as coordenadas de G são 0 0, 0 2 m, e sua velocidade é 0 (1,2 m/s)i (0,96 m/s)j. Pouco depois, o fio se rompe; observa-se então que o disco A se move ao longo de uma trajetória paralela ao eixo y e o disco B ao longo de uma trajetória que intercepta o eixo x a uma distância b 7,5 m de O. Determine (a) as velocidades de A e B após o fio se romper, (b) a distância a entre o eixo y e a trajetória de A.

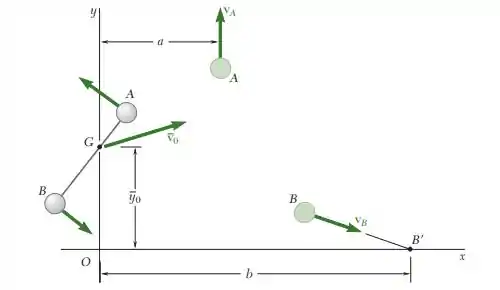
Passo 1

No primeiro passo podemos determinar a posição de G. O centro de massa pode ser calculado assim:

A G + G B = A B

Mas

A G m B = B G m A = A G + G B m B + m A = A B m = 0,6 4,5

Então

A G m B = 0,6 4,5

Logo

A G = 1,5 0,6 4,5 = 0,2   m

E, portanto,

B G = 0,6 - 0,2 = 0,4   m

Passo 2

Agora podemos calcular o momento linear inicial do sistema

L 0 = m v 0 → = 4,5 1,2   i ^ + 0,96   j ^

Então

L 0 = 5,4   i ^ + 4,32   j ^

E o momento angular fica

H G 0 = G A → × m A v A ' + G B → × m B v B '

Substituindo os valores

H G 0 = 0,2 3 0,2 × 10 + 0,4 1,5 0,4 × 10

Então

H G 0 = 3,6   k ^

Lá no problema 14.27 nós derivamos uma formula que vai ser útil aqui:

H O 0 = r → × m v 0 → + H G 0

H O 0 = 2   j ^ × 5,4   j ^ + 4,32   j ^ + 3,6   k ^

H O 0 = - 10,8   k ^ + 3,6   k ^ = - 7,2   k ^

E agora vamos calcular a energia cinética inicial

T 0 = 1 2 m v 0 2 + m A v A ' 2 + m B v B ' 2

T 0 = 1 2 ( 4,5 1,2 2 + 0,96 2 + 3 0,2 × 10 2 + 1,5 0,4 × 10 2

Então

T 0 = 5,3136 + 6 + 12 = 23,314   J

Passo 3

Agora vamos usar conservação de momento angular.

L 0 = L f

5,4   i ^ + 4,32   j ^ = m A v A + m B v B

5,4   i ^ + 4,32   j ^ = 3   v A j ^ + 1,5   v B x   i ^ + v B y   j ^

Resolvendo por coeficiente temos:

5,4 = 1,5   v B x

Então

v B x = 3.6 m s

Agora para j ^

4,32 = 3 v A + 1,5   v B y

Então

v B y = 2,88 - 2 v A

Agora vamos usar conservação de energia

T 0 = T f

23,314 = 1 2 m A v A 2 + m B v B 2

Substituindo os valores

23,314 = 1 2 3 v A 2 + 1,5 v B x     2 + v B y 2

Substituindo as velocidades

23,314 = 1 2 3 v A 2 + 1,5 3,6 2 + ( 2,88 - 2 v A 2 )  

Então

v A = 2,56 m s

Com esse resultado podemos calcular

v B y = 2,88 - 2 v A

v B y = 2,88 - 2 2,56

v B y = - 2,24 m s

Sendo assim temos

v A = 2,56   j ^ m s

v B = 3,6   i ^ - 2,24   j ^ m s  

Ou em módulo

v B = 4,24 m s

Passo 4

Agora vamos usar conservação de momento angular.

H O 0 = H O

- 7,2   k ^ = a i ^ × 3 2,56   j ^ + 7,5   i ^ × 1,5 3,6   i ^ - 2,24   j ^

Então

- 7,2   k ^ = 7,68 a   k ^ - 25,2   k ^

Logo

a = 2,34   m

Resposta

a : v A = 2,4 m s ; v B = 4,24 m s b :   a = 2,34   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O cascalho cai com velocidade zero em um transportador de correia com a taxa q = d m / d t constante. ( a ) Determine a intensidade da força P necessária para manter a velocidade da correia v constant
Um foguete tem 1.200k g de massa, incluindo 1.000k g de combustível, que é consumido à taxa de 12,5k g / s e ejetado com uma velocidade relativa de 4.000m / s . Sabendo que o foguete é lançado na vert
Determine o aumento da velocidade do satélite de comunicação do Problema 14.95 após 12,5k N de combustível tenha sido consumido.
Uma espaçonave que descreve uma órbita circular em torno da Terra a uma velocidade de 24 × 10 3k m / h libera sua cápsula frontal de 600k g de massa bruta que inclui 400k g de combustível. Sabendo que
Um satélite de comunicação de 50k N , incluindo o combustível, foi ejetado do ônibus espacial descrevendo uma órbita circular de baixa altitude em torno da terra. Depois que o satélite foi lentamente