O movimento de uma partícula carregada em um campo eletromagnético pode ser obtido pela equação de Lorentz para a força sobre uma partícula nesse tipo de campo. Se o vetor do campo elétrico é e o vetor do campo magnético é , a força sobre uma partícula de massa , com uma carga e velocidade é fornecida por:

Onde supomos que (velocidade da luz).

(a) Se não existe nenhum campo elétrico e se a partícula adentra o campo magnético em uma direção perpendicular às linhas de fluxo magnético, mostre que a trajetória é um círculo com raio:

Onde é a frequência de cíclotron.

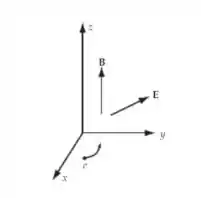
(b) Escolha o eixo na direção de e considere o plano e como o plano . Desse modo,

Demonstre que a componente do movimento é fornecida por:

Onde

(c) Continue o cálculo e obtenha expressões para e . Demonstre que as médias de tempo dessas componentes da velocidade são:

(Mostre que o movimento é periódico e calcule a média sobre um período completo.)

(d) Integre as equações de velocidade encontradas em (c) e demonstre (com as condições inicias , ),

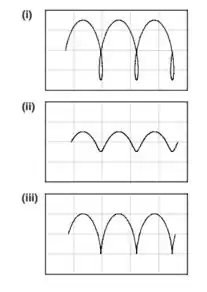
Essas são as equações paramétricas de um trocoide. Faça um gráfico da projeção da trajetória no plano – para os casos (i), (ii) e (iii) . O último caso produz um cicloide.

Letra (b)

Aqui não fazemos suposições sobre as orientações relativas de e , ou seja, a velocidade pode ter um componente na direção ao entrar na região do campo. Deixe , com e . Iremos calcular primeiro o termo .

Dessa forma a equação de Lorentz torna-se:

Reescrevendo isso como equações componentes:

Note que a equação do movimento componente é facilmente integrável, com as constantes de integração dadas pelas condições iniciais no enunciado do problema, assim temos:

Letras (c)

Somos solicitados a encontrar expressões para e , que chamaremos de e , respectivamente. Diferencie uma vez em relação ao tempo e substitua por :

Ou

Esta é uma equação diferencial não homogênea que tem tanto uma solução homogênea (a solução para a equação acima com o lado direito igual a zero) quanto uma solução particular. A solução mais geral é a soma de ambas, que neste caso é:

Onde e são constantes de integração. Este resultado pode ser substituído em para obter

Onde é outra constante de integração. É encontrado após a substituição em , no entanto, que devemos ter . Para calcular as médias de tempo, observe que tanto o seno quanto o cosseno têm um média de zero em um de seus períodos .

Letra (d)

Obtemos as equações paramétricas simplesmente integrando as equações de velocidade.

Onde, de fato, e são constantes de integração. Podemos agora avaliar todos os e usando nossas condições iniciais , , e . Isso nos dá: , e dá a resposta correta:

Esses casos são mostrados na figura como: casos (i), (ii) e (iii) .