Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 2.Problemas - Ex. 43

Uma partícula se encontra sob a influência de uma força F = - k x + k x 3 α 2 , onde k e α são constantes e k é positivo. Determine U(x) e discuta o movimento. O que ocorre quando E = (1/4)kα2?

Passo 1

E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de mecânica Newtoniana.

A partir da equação da força dada no enunciado:

U x = E p o t = - ∫ F d x = - ∫ - k x + k x 3 α 2 d x = 1 2 k x 2 - 1 4 k x 4 α 2

Para esboçar U(x), notamos que para x pequeno, U(x) se comporta como a parábola 1 2 k x 2 . Para x grande, o comportamento é determinado por - 1 4 k x 4 α 2 .

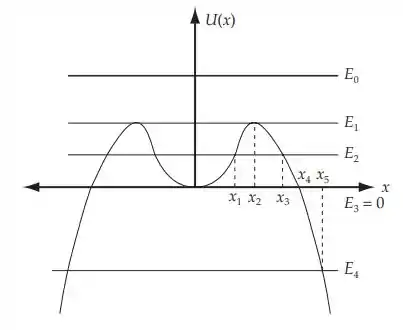
Para E = E0, o movimento é ilimitado; a partícula pode estar em qualquer lugar.

Para E = E1 (no máximo em U(x)) a partícula está em um ponto de equilíbrio instável. Ele pode permanecer em repouso onde está, mas se for levemente perturbado, ele se afastará do equilíbrio.

Passo 2

Qual é o valor de E1? Encontramos os valores de x para os quais dU/dx = 0.

- k x + k x 3 α 2 = 0 = > k x = k x 3 α 2 = > α 2 = x 2   o u   x = ± α

Daí temos que:

U ± α = E 1 = 1 2 k ± α 2 - 1 4 k ± α 4 α 2 = 1 2 k α 2 - 1 4 k α 2 = 1 4 k α 2

Para E = E2, a partícula é limitada e oscila entre −x2 e x2; ou a partícula vem de - ∞ para –x3 e retorna para - ∞ ou + ∞ para +x3 e retorna para + ∞ .

Para E3 = 0, a partícula está no ponto de equilíbrio estável em x = 0, ou além de x = ±x4.

Para E4, a partícula vem de ± ∞ para ± x 5 e retorna.

Resposta

Ver passo a passo.

Exercícios de Livros Relacionados

Um míssil é disparado do chão com uma velocidade inicial v 0 que faz um ângulo ϕ 0 com a vertical. Se o míssil tiver que alcançar uma altitude máxima igual a R , onde R é o raio da Terra, ( a ) mostre
Mostre que os valores v A e v P da velocidade de um satélite da Terra no apogeu A e no perigeu P de uma órbita elíptica estão definidos pelas relações v A 2 = 2 G M r A + r P r P r Av P 2 = 2 G M r A
Usando as respostas obtidas no Problema 13.107, mostre que a órbita circular pretendida e a órbita elíptica resultante interceptam-se nas extremidades do eixo menor da órbita elíptica.
Quando o módulo lunar foi deixado à deriva após o retorno de dois dos astronautas da Apollo ao módulo de comando, que orbitava a Lua a uma altitude de 140k m , sua velocidade foi reduzida para deixá--
Sabendo que a velocidade de uma sonda espacial experimental lançada da Terra tem intensidade v A = 32,32 × 10 3k m / h no ponto A , determine a velocidade da sonda quando ela passar pelo ponto B .