Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 154

O movimento de uma partícula é definido pelas equações x = ( 2 t + t 2 ) m e y = ( t 2 ) m, onde t é dado em segundos. Determine as componentes normal e tangencial da velocidade e aceleração da partícula quando t = 2   s .

Passo 1

O movimento da partícula é definido por

x = ( 2 t + t 2 )

y = ( t 2 )

Assim sendo, podemos escrever a trajetória como

s = 2 t + t 2 i + ( t 2 ) j

Devemos determinar as componentes normal e tangencial da velocidade e a aceleração da partícula em t = 2 s.

Primeiramente, vamos determinar a velocidade.

Sabemos que a velocidade vetorial é dada por

v = d s d t

Logo,

v = 2 + 2 t i + 2 t j

Para t = 2 s, temos

v = 6 i + 4 j

Onde a velocidade escalar será dada por

v = v x 2 + v y 2 = 6 2 + 4 2 = 7,21   m / s

Por definição, a velocidade é sempre tangente ao movimento. Logo

v n = 0

v t = v = 7,21   m / s

Passo 2

Para determinar a aceleração a vetorial, utilizaremos a relação

a = d v d t = 2 i + 2 j

Portanto, temos que

a = a x 2 + a y 2 = 2 2 + 2 2 = 2,828   m / s 2

Para descobrir as componentes de a tangencial e normal, devemos encontrar o ângulo ϕ que essas componentes fazem com o eixo de referência.

Par entender melhor a situação, desenhamos o diagrama de corpo livre da partícula.

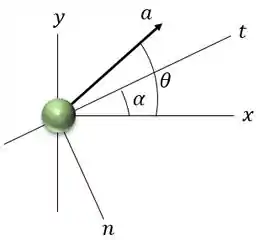
O ângulo será ϕ = θ - α .

Sabemos que, em t = 2 ,

α = tan - 1 ⁡ v y v x = tan - 1 ⁡ 4 6 = 33,69 °

θ = tan - 1 ⁡ a y a x = tan - 1 ⁡ 2 2 = 45 °

Logo,

ϕ = θ - α = 45 - 33,69 = 11,31 °

As componentes tangencial e normal da aceleração são:

a t = a cos ⁡ ϕ = 2,828 cos ⁡ 11,31 ° = 2,77   m / s 2

a n = a sen ⁡ ϕ = 2,828 sen ⁡ 11,31 ° = 0,555   m / s 2

Resposta

v n = 0

v t = v = 7,21   m / s

a t = 2,77   m / s 2

a n = 0,555   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As partículas A e B estão se deslocando em torno de uma pista circular a uma velocidade escalar de 8 m/s no instante mostrado. Se a velocidade escalar de B está aumentando na razão de a t B = 4m / s 2
Uma bola é chutada com velocidade escalar inicial v A = 8m / s a um ângulo θ A = 40 ° com a horizontal. Encontre a equação da trajetória, y = f ( x ) , e, em seguida, determine as componentes normal e
Dois ciclistas, A e B, estão se deslocando no sentido anti-horário em torno de uma pista circular a uma velocidade escalar constante de 2,4m / s no instante mostrado. Se a velocidade escalar de A é au
As partículas A e B estão se deslocando no sentido anti-horário em torno de uma pista circular a uma velocidade escalar constante de 8m / s . Se no instante mostrado a velocidade de A é aumentada na r