Um carro move-se sobre um morro descrito por . Se ela tem uma velocidade escalar constante de 22,5 m/s, determine as componentes e da velocidade e aceleração da camionete quando

Podemos representar a magnitude da velocidade da pela seguinte equação:

Substituimos e a nova equação encontrada no passo 1, temos:

Isolando nós encontramos o seguinte resultado:

Substituimos este resultado na equação encontrada no passo 1:

Assim como fizemos no passo 1, podemos encontrar uma relação entre os componentes e da aceleração da partícula calculando a segunda derivada da equação da trajetória da partícula. Para isso, usaremos a regra da cadeia no processo de derivação.

Ou podemos escrever da seguinte forma:

Para e , temos o seguinte:

Note que a partícula viaja com velocidade constante, desta forma, sua aceleração ao longo da tangente do trajeto é igual a 0. Note também, que o ângulo que a tangente faz com o eixo horizontal em é:

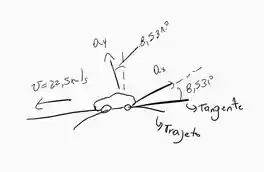
no ponto

ponto

Formaremos um sistema com esta equação e a equação encontrada no passo 4. Resolvendo, encontramos:

e