Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 150

As partículas A e B estão se deslocando em torno de uma pista circular a uma velocidade escalar de 8 m/s no instante mostrado. Se a velocidade escalar de B está aumentando na razão de a t B = 4   m / s 2 e no mesmo instante A tem um aumento na velocidade escalar na razão de a t A = 0,8 t   m / s 2 , determine quanto tempo leva para ocorrer uma colisão. Qual a intensidade da aceleração de cada partícula pouco antes de ocorrer a colisão?

Passo 1

O enunciado nos dá as seguintes informações:

Velocidade das partículas A e B : v = 8   m / s ;

Aceleração de B : a t B = 4   m / s 2 ;

Aceleração de A :   a t A = 0,8 t   m / s 2 ;

Raio de curvatura: ρ = r = 5   m .

Devemos determinar quanto tempo leva para ocorrer uma colisão entre as partículas e qual é a intensidade da aceleração de cada uma pouco antes da colisão.

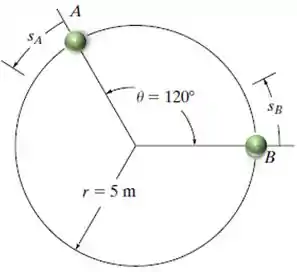
Analisando a imagem dada, vemos que o na posição inicial, o ângulo entre as partículas é de θ = 120 ° . Sabemos que o comprimento de um arco é dado por

d = ρ θ

Onde θ está em radianos.

Logo, a distância entre as partículas A e B é de

d = 5 120 ° π 180 ° = 10,74   m

Passo 2

Primeiramente, vamos avaliar a distância percorrida pelas partículas.

Podemos obter a distância deslocada por B através da seguinte equação pois a aceleração desta partícula é constante:

s = s 0 + v 0 t + 1 2 a t 2

s B = s 0 B + v 0 B t + 1 2 a B t 2

s B = 0 + 8 t + 1 2 ( 4 ) t 2

s B = 2 t 2 + 8 t

A aceleração da partícula A está em função de t , portanto a distância deslocada por ela pode ser obtida através da integração de a = d v / d t , seguida da integração de v = d s / d t . Temos que

a A = d v A d t

d v A = a A   d t

∫ 8 v A d v A = ∫ 0 t 0,8 t   d t

v A = 0,4 t 2 + 8

Temos que

v A = d s A d t

d s A = v A   d t

∫ 0 s A d s = ∫ 0 t 0,4 t 2 + 8   d t

s A = 0,4 t 3 3 + 8 t

Para a colisão ocorrer, a distância percorrida por A , mais a distância entre as partículas, deve ser menor ou igual ao deslocamento sofrido pela partícula B . Logo,

s A + d = s B

0,4 t 3 3 + 8 t + 10,74 = 2 t 2 + 8 t

0,4 t 3 3 - 2 t 2 + 10,74 = 0

Esta equação de terceito grau possui duas raízes positivas: t = 2,54   e   t = 14,62 . A primeira colisão ocorrerá em t = 2,54 pela partícula B em A . Em t = 14,62 ocorrerá a colisão da partícula A em B . Como a questão pede para determinarmos o tempo até a primeira colisão, vamos utilizar t = 2,54 s.

Passo 3

Agora vamos determinar a intensidade da aceleração para cada partícula.

Para partícula A :

A aceleração tangencial em t = 2,54   s é

a t A = 0,8 t = 2,032   m / s 2

A velocidade é

v A = 0,4 t 2 + 8 = 10,58   m / s

A aceleração normal é dada por a n = v 2 / ρ . Logo,

a n A = v A 2 ρ = 22,39   m / s 2

A magnitude da aceleração de A é

a A 2 = a t A 2 + a n A 2

a A = 22,5   m / s 2

Para partícula B :

A aceleração tangencial em t = 2,54   s é

a t B = 4   m / s 2

A velocidade é

v B = v 0 + a t = 8 + 4 2,54 = 18,46   m / s

A aceleração normal é dada por a n = v 2 / ρ . Logo,

a n B = v B 2 ρ = 65,96   m / s 2

A magnitude da aceleração de A é

a B 2 = a t B 2 + a n B 2

a B = 66,1   m / s 2

Resposta

t = 2,54   s

a A = 22,5   m / s 2

a B = 66,1   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os anéis estão conectados por um pino em B e estão livres para se mover ao longo da barra O A e da guia curvilínea O C , tendo o formato de uma cardinoide, r = 0,2 1 + cos ⁡ θ m. Em θ = 30 ° , a veloc
No instante que θ = 45 ° , o atleta está correndo com uma velocidade escalar constante de 2 m/s. Determine a velocidade angular na qual a câmera deve girar a fim de seguir o movimento.
A posição de uma partícula é descrita por r = t 3 + 4 t - 4 m e θ = t 3 / 2 rad, onde t é dado em segundos. Determine as intensidades da velocidade e aceleração da partícula no instante t = 2 s.
Uma partícula move-se ao longo de uma trajetória circular de raio 300 mm. Se sua velocidade angular é θ ˙ = 2 t 2 rad/s, onde t é dado em segundo, determine a intensidade da aceleração da partícula qu
Uma partícula move-se ao longo de uma trajetória circular de raio 5 m. Se sua posição é θ = e 0,5 t rad, onde t é dado em segundos, determine a intensidade da aceleração da partícula quando θ = 90 ° .