Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 149

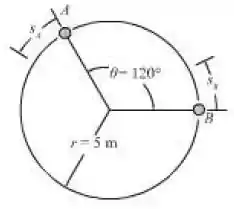
As partículas A e B estão se deslocando no sentido anti-horário em torno de uma pista circular a uma velocidade escalar constante de 8   m / s . Se no instante mostrado a velocidade de A é aumentada na razão de a t A = 0,4   s A   m / s 2 , onde s A é dado em metros, determine a distância medida no sentido anti-horário ao longo da pista de B para A quando t = 1   s . Qual é a intensidade da aceleração de cada partícula neste instante?

Passo 1

Vamos começar com bastante calma. A distância inicial entre as partículas é dada pelo comprimento do arco de circunferência, isto é:

d 0 = θ r = 2 π 3 ⋅ 5 = 10 π 3   m

Agora, precisamos calcular as posições finais e iniciais das partículas. Para o caso da partícula B, será mais fácil. Se ele tem uma velocidade constante, então:

s B = v B t = 8   m

Agora, para o ponto A será um pouco mais complicado. Precisaremos trabalhar com as equações da cinemática para podermos determinar a sua posição.

Já para determinar a aceleração, será um pouco mais fácil. Basta que não esqueçamos da componente normal da aceleração

Passo 2

Para podermos determinar a posição final da partícula A, precisamos começar relacionando a velocidade com a sua posição. Portanto, temos a seguinte relação:

∫ 8 v A v d v = ∫ 0 s A a t A d s

v A 2 - 64 2 = ∫ 0 s A 0 , 4 s A d s

v A = 0 , 4 s A 2 + 64

Agora, precisamos relacionar esta equação acima com o tempo. Para isto, temos:

v = d s A d t = 0 , 4 s A 2 + 64

∫ 0 s A d s A 0 , 4 s A 2 + 64 = ∫ 0 t d t

1 0,6325 sen - 1 ⁡ s A 12,65 = t

Quando t = 1   s , temos:

s A = 8 , 66   m

Portanto, a distância entre os ciclistas é:

d = d 0 + s A - s B = 1 1 , 13   m

Passo 3

Vamos calcular as acelerações dos ciclistas. Para o caso do ciclista A, temos aceleração normal e tangencial. Portanto,

a t A = 0 , 4 s A = 3,464   m / s 2

a n A = v A 2 ρ = 0 , 4 ⋅ 8,66 2 + 64 5 = 18,8   m / s 2

a A = a n A 2 + a t A 2 = 19,12   m / s 2

Já para o ciclista B, temos:

a t B = 0

a n B = v B 2 ρ = 64 5 = 12,8   m / s 2

a B = a n B 2 + a t B 2 = 12,8   m / s 2

Resposta

d = 11,13   m

a A = 19,12   m / s 2

a B = 12,8   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

2/126) Um jogador de beisebol lança uma bola com as condições iniciais mostradas na figura . Determine o raio de curvatura da trajetória (a) logo após o lançamento e (b) no ápice . Para cada caso , ca
O cometa Halley viaja em uma órbita elíptica alongada cuja distância mínima do Sol é aproximadamente rE, onde rE 150x 106 km é a distância média do Sol à Terra. Sabendo que o período do cometa Halley
Com base em observações feitas durante a aparição de 1996 do cometa Hyakutake, concluiu-se que a trajetória desse cometa é uma elipse muito alongada para a qual a excentricidade é de aproximadamente 0
Determine o tempo necessário para uma sonda espacial do Problema 12.99 viajar de B para C.
Uma sonda espacial está descrevendo uma órbita circular de raio nR com uma velocidade escalar v0 ao redor de um planeta de raio R e centro O. Quando ela passa pelo ponto A, sua velocidade escalar é re