Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 93

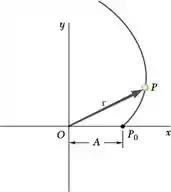
O movimento de uma partícula está definido pelo vetor de posição r = A(cos t + t sen t)i + A(sen t - t cos t)j, onde t e expresso em segundos. Determine os valores de t para os quais o vetor de posição e o vetor de aceleração são (a) perpendiculares e (b) paralelos.

Passo 1

E ai galera tudo certinho? O enunciado pede que a gente encontre quais o vetor de posição e o vetor de aceleração são (a) perpendiculares e (b) paralelos.

Nós temos

r = A cos ⁡ t + t sin ⁡ t i + A sin ⁡ t - t cos ⁡ t j

Então

v = d r d t = A - sin ⁡ t + sin ⁡ t + t cos ⁡ t i

+ A cos ⁡ t - cos ⁡ t + t sin ⁡ t j

= A t cos ⁡ t i + A t sin ⁡ t j

e

a = d v d t = A cos ⁡ t - t sin ⁡ t i + A sin ⁡ t + t cos ⁡ t j

Passo 2

  1. Quando r e a são perpendiculares, r ∙ a = 0

    2. A cos ⁡ t + t sin ⁡ t i + sin ⁡ t - t cos ⁡ t j ∙ A cos ⁡ t - t sin ⁡ t i + sin ⁡ t + t cos ⁡ t j = 0

    ou

    cos ⁡ t + t sin ⁡ t cos ⁡ t - t cos ⁡ t + sin ⁡ t - t cos ⁡ t sin ⁡ t + t cos ⁡ t = 0

    ou

    cos 2   t - t 2   sin 2   t + sin 2   t - t 2   cos 2   t = 0

    Passo 3

  2. Quando r e a são paralelos, r × a = 0.

A cos ⁡ t + t sin ⁡ t i + sin ⁡ t - t cos ⁡ t j ∙ A cos ⁡ t - t sin ⁡ t i + sin ⁡ t + t cos ⁡ t j = 0

ou

cos ⁡ t + t sin ⁡ t sin ⁡ t + t cos ⁡ t - sin ⁡ t - t cos ⁡ t cos ⁡ t - t sin ⁡ t k = 0

Expandindo

sin ⁡ t cos ⁡ t + t + t 2 sin ⁡ t cos ⁡ t - sin ⁡ t cos ⁡ t - t + t 2 sin ⁡ t cos ⁡ t = 0

Resposta

a)  1 - t 2 = 0             ou           t = 1   s

b) 2 t = 0             ou             t = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma jogadora de basquete arremessa a bola a 5 m da tabela. Sabendo que a bola tem uma velocidade inicial v0 em um ângulo de 30° com a horizontal, determine o valor de v0 quando d é igual a (a) 0,2 m e
A areia é descarregada em A pela correia transportadora e cai no topo de uma pilha em B. Sabendo que a correia transportadora forma um ângulo de 20° com a horizontal, determine a velocidade v0 da corr
Uma bola é solta sobre um degrau no ponto A e quica com uma velocidade inicial v0 a um ângulo de 15° com a vertical. Determine o valor de v0 sabendo que, no instante imediatamente anterior ao da bola
O leite é derramado no copo de vidro com altura de 140 mm e com diâmetro interno de 66 mm. Se a velocidade inicial do leite é 1,2 m/s em um ângulo de 40° com a horizontal, determine o intervalo de val
Um irrigador oscilante de jardim, que lança um jato de água com uma velocidade inicial v0 de 8 m/s, é usado para irrigar uma horta. Determine a distância d para o ponto mais afastado B que será irriga