Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.6 - Ex. 147

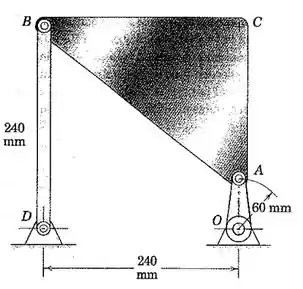
O movimento plano da placa triangular ABC é controlado pela manivela AO e pela barra DB. Para o instante representado, quando AO e DB são verticais, AO possui uma velocidade angular no sentido horário de 3 rad/s e uma aceleração angular no sentido anti-horário de 10 rad/s². Determine a aceleração angular de DB para esse instante.

Passo 1

Pessoal, primeiro vamos organizar todos os dados do enunciado e fazer um esboço do mecanismo.

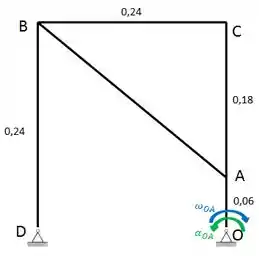
Podemos calcular a velocidade e aceleração do ponto A neste instante:

v A = ω A O × r A O = - 3 k ^ × 0,06 j ^ = 0,18 i ^   r a d / s

a A = - r A O ω A O 2 + α A O × r A O = - 3 2 0,06 j ^ + 10 k ^ × ( 0,06 j ^ )

a A = - 0 , 6 i ^ - 0 , 54 j ^   m / s 2

Da mesma forma, podemos calcular para o ponto B, pegando como referência a barra DB. Mas antes é importante notar que neste instante vale a relação v A = v B = 0,18 i ^   r a d / s (dica, caso não lembre: use a velocidade relativa v B = v A + ω A B × r B A , e decomponha em i e j).

v B = ω B D × r B D → ω B D = - 0,18 0,24 = - 0,75   k ^   r a d / s

a B = - r B D ω B D 2 + α B D × r B D = - ( 0,75 ) 2 0 , 24 j ^ + α B D k ^ × ( 0 , 24 j ^ )

a B = - 0 , 24 α B D i ^ - 0,135 j ^   m / s 2

Passo 2

Neste passo, vamos usar a equação da aceleração relativa para os pontos A e B.

a B = a A + a B / A n + a B / A t

Agora, vamos substituir os valores encontrados na equação acima:

- 0,24 α B D i ^ - 0,135 j ^ = - 0,6 i ^ - 0,54 j ^ + 0 + ( - 0,18 i ^ - 0,24 j ^ ) α A B

Decompondo nas direções, temos o sistema:

- 0,24 α B D i ^ = - 0,6 i ^ - 0,18 α A B

- 0,135 j ^ = - 0,54 j ^ - 0,24 j ^ α A B

Resolvendo o sistema, temos a resposta do problema:

α A B = - 1,688   k ^   r a d / s 2

α B D = 1,234   k ^   r a d / s 2

Resposta

α B D = 1,234   k ^   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A placa retangular mostrada na figura gira à taxa constante ω 2 = 12r a d / s em relação ao braço A E , que, por sua vez, gira à taxa constante ω 1 = 9r a d / s em torno do eixo Z . Para a posição mos
Usando o método da Seção 15.14 , resolva o Problema 15.191 .
Usando o método da Seção 15.14 , resolva o Problema 15.19 5 .
Uma placa quadrada com 500m m de lado está articulada nos pontos A e B de um grampo em U . A placa gira à taxa constante ω 2 = 4r a d / s em relação ao grampo, que, por sua vez, gira à taxa constante
O rotor de um motor elétrico tem a velocidade de 1.800 rpm quando a energia é desligada. O rotor é então observado até alcançar o repouso após executar 1.550 rpm. Considerando o movimento uniformement